Question

【题目】已知数列的前项和为，且.

(1)求数列的通项公式，并写出推理过程；

(2)令，，试比较与的大小，并给出你的证明.

Answer 1

【答案】（Ⅰ）；（Ⅱ），证明见解析．

【解析】试题分析：（Ⅰ）由题意可根据数列通项与前项和之间的关系来进行求解，即当时，；当时，，这时可得到与的关系式，根据关系式的特点，可通过构造换元，令，从而得出数列是等差数列，先求出数列的通项，再求出数列的通项；（Ⅱ）根据数列的特点可利用错位相减法求出，接着利用作差法进行比较，根据差式的特点这里可采用数学归纳法进行猜想证明，详见解析．

试题解析：（Ⅰ）在中，令，可得，即，

当时，，∴，

∴，即，

设，则，即当时，，

又，∴数列是首项和公差均为1的等差数列．

于是，∴

（Ⅱ）由（Ⅰ）得，

所以，

由①-②，

得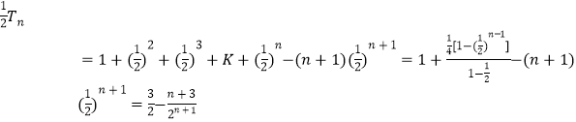

∴，则

于是只要比较与的大小即可，

（1）当时，，此时，即，

（2）猜想：当时，，下面用数学归纳法证明：

①当时，不等式成立；②假设时，不等式成立，即；

则当时，，

所以当时，不等式成立，

由①和②可知，当时，成立，

于是，当时，，即．

另证：要证，只要证：，只要证：，

由均值不等式得：，

所以，于是当时，，即．