题目内容

|x+2|+|x﹣3|的取值范围是　　．

考点：

函数的值域．

专题：

计算题．

分析：

先令f（x）=|x+2|+|x﹣3|=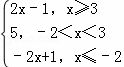，根据分段函数的性质可求值域

解答：

解：令f（x）=|x+2|+|x﹣3|=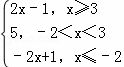

∵x≥3，2x﹣1≥5；x≤﹣2时，﹣2x+1≥5

根据分段函数的性质 可知，f（x）的取值范围f（x）≥5

故答案为：[5，+∞）

点评：

本题主要考查了函数的值域的求解，解题的关键是对已知函数去绝对值的化简

练习册系列答案
相关题目
对于定义在D上的函数y=f（x），若同时满足．
①存在闭区间[a，b]⊆D，使得任取x1∈[a，b]，都有f（x1）=c （c是常数）；
②对于D内任意x2，当x2∉[a，b]时总有f（x2）＞c称f（x）为“平底型”函数．
（1）（理）判断f1（x）=|x-1|+|x-2|，f2（x）=x+|x-2|是否是“平底型”函数？简要说明理由；
（文）判断f1（x）=|x-1|+|x-2|，f2（x）=x-|x-3|是否是“平底型”函数？简要说明理由；
（2）（理）设f（x）是（1）中的“平底型”函数，若|t-k|+|t+k|≥|k|•f（x），k∈R且k≠0，对一切t∈R恒成立，求实数x的范围；
（文）设f（x）是（1）中的“平底型”函数，若|t-1|+|t+1|≥f（x），对一切t∈R恒成立，求实数x的范围；
（3）（理）若F（x）=mx+
x2+2x+n
，x∈[-2，+∞）是“平底型”函数，求m和n的值；
（文）若F（x）=m|x-1|+n|x-2|是“平底型”函数，求m和n满足的条件．
1、已知全集U=R，M={x|-2≤x≤2}，N={x|x＜1}，那么M∩N=（　　）
1、已知集合M={x|-2≤x＜2}，N={x|y=log2（x-1）}，则M∩N=（　　）
下列说法中：
①若定义在R上的函数f（x）满足f（x+2）=-f（x-1），则6为函数f（x）的周期；
②若对于任意x∈（1，3），不等式x2-ax+2＜0恒成立，则a＞
11
3
；
③定义：“若函数f（x）对于任意x∈R，都存在正常数M，使|f（x）|≤M|x|恒成立，则称函数f（x）为有界泛函．”由该定义可知，函数f（x）=x2+1为有界泛函；
④对于函数f(x)=
x-1
x+1
，设f2（x）=f[f（x）]，f3（x）=f[f2（x）]，…，fn+1（x）=f[fn（x）]（n∈N*且n≥2），令集合M={x|f2009（x）=x，x∈R}，则集合M为空集．
正确的个数为（　　）
A、1个B、2个C、3个D、4个
下列说法中：
①若定义在R上的函数f（x）满足f（x+2）=-f（x-1），则6为函数f（x）的周期；
②若对于任意x∈（1，3），不等式x2-ax+2＜0恒成立，则a＞
11
3
；
③定义：“若函数f（x）对于任意x∈R，都存在正常数M，使|f（x）|≤M|x|恒成立，则称函数f（x）为有界泛函．”由该定义可知，函数f（x）=x2+1为有界泛函；
④对于函数f(x)=
x-1
x+1
，设f2（x）=f[f（x）]，f3（x）=f[f2（x）]，…，fn+1（x）=f[fn（x）]（n∈N*且n≥2），令集合M={x|f2009（x）=x，x∈R}，则集合M为空集．
正确的个数为（　　）
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网