Question

已知a、b、c∈R⁺,且a+b+c=1,

求证：（≥8.

Answer 1

分析：这是一个条件不等式的证明问题，要注意观察不等式的结构特点和条件a+b+c=1的合理应用.可用综合法和分析法两种方法证明.

证法一：(综合法）

（-1）(-1)(-1)

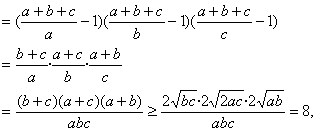
当且仅当a=b=c时取等号，所以不等式成立.

证法二:(分析法)

要证（-1）(-1)(-1)≥8成立，

只需证≥8成立.

因为a+b+c=1,

所以只需证≥8成立，

即≥8.

只需证≥8成立.

而≥8显然成立,

∴≥8成立.

绿色通道:

综合法是从已知条件出发，经过逐步推理，最后达到待证的结论；而在分析法中，从结论出发的每一个步骤所得到的判断都是使结论成立的充分条件，最后一步归结到已被证明了的事实或已知.

在证明不等式时要注意应用重要不等式和不等式的性质，要注意基本不等式应用的条件及等号成立的条件.