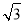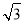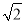题目内容
设F1,F2分别是双曲线 =1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使(
=1(a>0,b>0)的左、右焦点,若双曲线右支上存在一点P,使( +
+ )·
)· =0,O为坐标原点,且
=0,O为坐标原点,且 =
= |
| |,则双曲线的离心率为( ).
|,则双曲线的离心率为( ).
A.  +1 B.
+1 B. 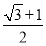 C.
C.  D.
D. 
A
【解析】由( +
+ )·
)· =0,得(
=0,得( +
+ )·(
)·( -
- )=0,即|
)=0,即| |2-|
|2-| |2=0,所以|
|2=0,所以| |=|
|=| |=c,所以△PF1F2中,边F1F2上的中线等于|F1F2|的一半,则PF1⊥PF2.即|PF1|2+|PF2|2=4c2,又
|=c,所以△PF1F2中,边F1F2上的中线等于|F1F2|的一半,则PF1⊥PF2.即|PF1|2+|PF2|2=4c2,又 =
= |
| |,解得|PF1|=
|,解得|PF1|= c,|PF2|=c,又|PF1|-|PF2|=
c,|PF2|=c,又|PF1|-|PF2|= c-c=2a.所以
c-c=2a.所以 =
= =
= +1=e.
+1=e.

练习册系列答案
相关题目