题目内容
15.下列函数在(0,+∞)上为减函数的是( )| A. | y=cosx | B. | y=-x2+2x | C. | $y={log_{\frac{1}{2}}}(x-1)$ | D. | y=e-x |
分析 根据题意,依次分析选项中函数的单调性,综合即可得答案.
解答 解:根据题意,依次分析选项:
对于A、y=cosx为余弦函数,单调递减区间为(2kπ,2kπ+π),在(0,+∞)上不是减函数,不符合题意;
对于B、y=-x2+2x是二次函数,单调递减区间为(1,+∞),不符合题意;
对于C、y=$lo{g}_{\frac{1}{2}}$(x-1)的定义域为(1,+∞),在(0,+∞)上不是减函数,不符合题意;
对于D、y=e-x=($\frac{1}{e}$)x,为指数函数,在R上递减,符合题意;
故选:D.
点评 本题考查函数单调性的判定,关键掌握常见函数的单调性.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
6.若10x=3,10y=4,则10x+y的值为( )
| A. | 700 | B. | 300 | C. | 400 | D. | 12 |
20.某市拟招商引资兴建一化工园区,新闻媒体对此进行了问卷调查,在所有参与调查的市民中,持“支持”、“保留”和“不支持”态度的人数如表所示:
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取部分市民做进一步调研(不同态度的群体中亦按年龄分层抽样),已知从“保留”态度的人中抽取了19人,则在“支持”态度的群体中,年龄在30岁以上的人有多少人被抽取;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
| 支持 | 保留 | 不支持 | |
| 30岁以下 | 900 | 120 | 280 |
| 30岁以上(含30岁) | 300 | 260 | 140 |
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取6人做进一步的调研,将此6人看作一个总体,在这6人中任意选取2人,求至少有1人在30岁以上的概率.
4.从长方体一个顶点出发的三条棱长分别为2、3、4,则其对角线的长为( )
| A. | 3 | B. | 5 | C. | $\sqrt{26}$ | D. | $\sqrt{29}$ |
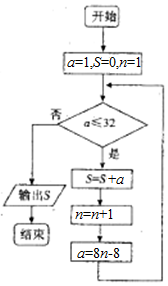 我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( )
我国古代数学著作《孙子算经》中有如下的问题:“今有方物一束,外周有三十二枚,问积几何?”设每层外周枚数为a,如图是解决该问题的程序框图,则输出的结果为( ) 如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.
如图,在多面体ABCDPE中,四边形ABCD和CDPE都是直角梯形,AB∥DC,∥DC,AD⊥DC,PD⊥平面ABCD,AB=PD=DA=2PE,CD=3PE,F是CE的中点.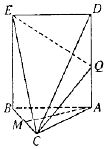 如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点
如图,ABED是长方形,平面ABED⊥平面ABC,AB=AC=5,BC=BE=6,且M是BC的中点