题目内容
已T=4为函数f（x）的一个周期，且f(x)=
．则方程3f（x）=x的解的个数为（ ）
|
分析：要求方程3f（x）=x的解的个数，只要分别作出函数y=f（x）与y=
x的图象，结合图象观察两函数的图象的交点个数即可求解方程的根的个数
| 1 |
| 3 |
解答：解：y1=
则x2+
=1表示焦点在y轴上的椭圆的上半部分，作出函数f（x）的图象如图所示
结合函数的图象可知y=f（x）与y=
x的图象有5个交点
∴3f（x）=x的解的个数为5个
故选B
| 7-7x2 |
| y2 |
| 7 |
结合函数的图象可知y=f（x）与y=
| 1 |
| 3 |
∴3f（x）=x的解的个数为5个
故选B
点评：本题主要考查了方程的根的个数的判断，主要转化为函数的交点的个数，解题的关键是利用周期性准确作出函数的图象
练习册系列答案
相关题目
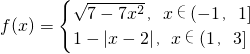．则方程3f（x）=x的解的个数为
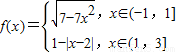．则方程3f（x）=x的解的个数为（ ）