题目内容
4.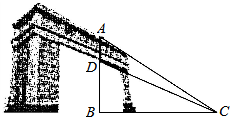 某大学的大门蔚为壮观,有个学生想搞清楚门洞拱顶D到其正上方A点的距离,他站在地面C处,利用皮尺量得BC=9米,利用测角仪测得仰角∠ACB=45°,测得仰角∠BCD后通过计算得到sin∠ACD=$\frac{\sqrt{26}}{26}$,则AD的距离为( )
某大学的大门蔚为壮观,有个学生想搞清楚门洞拱顶D到其正上方A点的距离,他站在地面C处,利用皮尺量得BC=9米,利用测角仪测得仰角∠ACB=45°,测得仰角∠BCD后通过计算得到sin∠ACD=$\frac{\sqrt{26}}{26}$,则AD的距离为( )| A. | 2米 | B. | 2.5米 | C. | 3米 | D. | 4米 |
分析 根据已知条件求出AB=BC=9米,再根据在Rt△BDC中,BD=tan(45°-∠ACD)•BC,求出BD的值,最后根据AD=AB-BD,即可得出答案.
解答 解:∵Rt△ACB中,∠ACB=45°,
∴BC=AB=9,
∵sin∠ACD=$\frac{\sqrt{26}}{26}$,
∴可解得cos∠ACD=$\frac{5\sqrt{26}}{26}$,tan∠ACD=$\frac{1}{5}$,
∵在Rt△BDC中,BD=tan(45°-∠ACD)•BC=9×$\frac{1-\frac{1}{5}}{1+\frac{1}{5}}$=6,
∴AD=AB-BD=9-6=3(米),
∴AD的距离为3米.
故选:C.
点评 本题考查仰角的定义,以及解直角三角形的实际应用问题.此题难度不大,解题的关键是要求学生能借助仰角构造直角三角形并解直角三角形,注意当两个直角三角形有公共边时,利用这条公共边进行求解是解此类题的常用方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知函数f(x)是周期为2的函数,当-1≤x≤1时,f(x)=$\left\{\begin{array}{l}{{x}^{2},-1≤x<0}\\{kx-1,0≤x≤1}\end{array}\right.$,则f($\frac{17}{4}$)=( )
| A. | 0 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{4}$ |
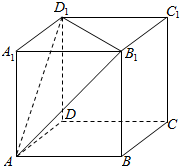 如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$.
如图所示,正方体ABCD-A1B1C1D1的棱长为6,则以正方体ABCD-A1B1C1D1的中心为顶点,以平面AB1D1截正方体外接球所得的圆为底面的圆锥的全面积为$24π+18\sqrt{2}π$.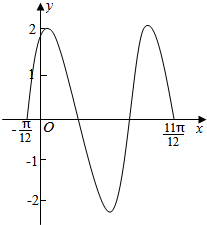 已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示:
已知函数f(x)=2sin(ωx+φ)(ω>0,0<φ<$\frac{π}{2}$)的图象如图所示: