题目内容
设向量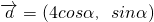
，
，
，
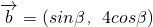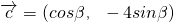（1）若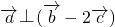
，求tan（α+β）的值
（2）若tanαtanβ=16，证明：
．
解：（1）向量，，，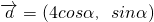
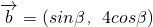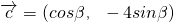因为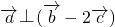，所以
，
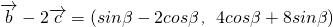4cosα（sinβ-2cosβ）+sinα（4cosβ+8sinβ）=0，
可得4cosαsinβ-8cosαcosβ+4sinαcosβ+8sinαsinβ=0，
∴4sin（α+β）-8cos（α+β）=0
所以tan（α+β）=2．
（2）∵tanαtanβ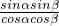=16，
=16，
即sinαsinβ=16cosαcosβ，
即sinα•sinβ-4cosα•4cosβ
所以成立．命题得证
分析：（1）求出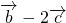
，通过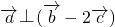，数量积为0，求tan（α+β）的值
（2）通过tanαtanβ=16，化为弦函数，利用两个向量的坐标运算，然后证明．
点评：本题考查平面向量的数量积的计算，两角和的正弦函数的应用，向量共线的坐标运算，考查计算能力．
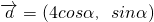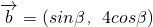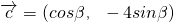，，，因为
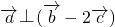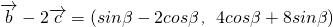，所以，4cosα（sinβ-2cosβ）+sinα（4cosβ+8sinβ）=0，
可得4cosαsinβ-8cosαcosβ+4sinαcosβ+8sinαsinβ=0，
∴4sin（α+β）-8cos（α+β）=0
所以tan（α+β）=2．
（2）∵tanαtanβ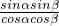=16，
=16，即sinαsinβ=16cosαcosβ，
即sinα•sinβ-4cosα•4cosβ
所以
成立．命题得证分析：（1）求出
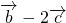，通过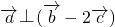，数量积为0，求tan（α+β）的值（2）通过tanαtanβ=16，化为弦函数，利用两个向量的坐标运算，然后证明
．点评：本题考查平面向量的数量积的计算，两角和的正弦函数的应用，向量共线的坐标运算，考查计算能力．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目
，
，
．
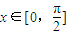，求x的值；
，求f（x）的最大值．
，
，
．
，求x的值；
，求f（x）的最大值．
，
，
．
∥
，求证：△ABC为等腰三角形；
⊥
，边长c=2，角C=
，求△ABC的面积．
，
，
．
∥
，求证：△ABC为等腰三角形；
⊥
，边长c=2，角C=
，求△ABC的面积．
，
，
．
∥
，求证：△ABC为等腰三角形；
⊥
，边长c=2，角C=
，求△ABC的面积．