Question

如图，在正方体ABCD-A₁B₁C₁D₁中E、F分别为棱DD₁、BB₁上的动点，且BF=D₁E，设EF与AB所成角为α，EF与BC所成的角为β，则α+β的最小值为（　　）

A．45°

B．60°

C．90°

D．无法确定

Answer 1

分析：在平面AA₁B₁B中过点E作直线EM∥AB，交AA₁于点M，连接MF，可得∠MEF=α，同理可得α=β．Rt△MFE中算出EF关于λ的式子，从而得到cosα的取值范围，结合余弦函数单调性求出α的取值范围，可得α+β的取值范围，得到α+β的最小值．

解答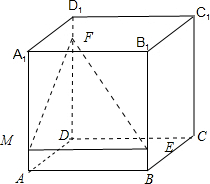：解：在平面AA₁B₁B中过点E作直线EM∥AB，交AA₁于点M，连接MF，
则可得∠MEF就是异面EF、AB所成角，即∠MEF=α，
同理可得EF与BC所成的角β=α．
设BF=D₁E=λ（0＜λ＜1），正方体ABCD-A₁B₁C₁D₁的棱长等于1，则
在Rt△MFE中，ME=1，EF=

2+(1-2λ)2

，
∴cosα=

ME

EF

=

1

2+(1-2λ)2

≥

2

2

，
当λ=

1

2

时，cosα的最小值为

2

2

∵α为锐角或直角，∴α≤45°，可得α=β≤45°
因此，α+β的最小值为90°．
故选：C

点评：本题给出正方体ABCD-A₁B₁C₁D₁中的动线段EF，求EF与AB、BC所成角和的最小值．着重考查了正方体的性质和异面直线所成角求法等知识，属于中档题．