题目内容
(09年济宁质检一理)(12分)
已知函数![]() .
.
(Ⅰ)当![]() 时,
时,![]() 使不等式
使不等式![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
解析:(Ⅰ)当![]() 时
时![]() ,
,![]()
由![]() ,
,![]() 得函数
得函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则当![]() 时
时![]() 。
。
故要使![]() 使不等式
使不等式![]() 成立,只需
成立,只需![]() 即可。
即可。
(Ⅱ)在区间![]() 上,函数
上,函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方等价于
的下方等价于
对![]() ,
,![]()
![]() ,即
,即![]() 恒成立。
恒成立。
设![]() ,
,
则![]() .
.
当![]() 时,
时,![]() .
.
(1)若![]() ,即
,即![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 为减函数,
为减函数,
则当![]() 时
时![]() ,
,
只需![]() ,即当
,即当![]() 时
时![]() 恒成立.
恒成立.
(2)若![]() ,即
,即![]() 时,令
时,令![]() 得
得![]()
函数![]() 在区间
在区间![]() 为减函数,
为减函数,![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
(3)若![]() ,即当
,即当![]() 时
时![]() ,函数
,函数![]() 在区间
在区间![]() 为增函数,
为增函数,
则![]() ,不合题意.
,不合题意.
综上可知当![]() 时
时![]() 恒成立,
恒成立,
即当![]() 时,在区间
时,在区间![]() 上函数
上函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方。
的下方。
另解:对![]() ,
,![]()
![]() 恒成立,
恒成立,
即对![]() ,
,![]() 恒成立.
恒成立.
设函数![]() ,
,![]()
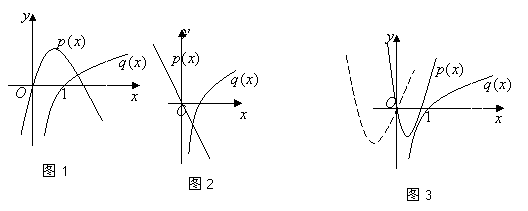
(1)如图1,当![]() 时,即
时,即![]() ,函数
,函数![]() 为开口向下的二次函数,
为开口向下的二次函数,
则当![]() 时,函数
时,函数![]() 的图象在
的图象在![]() 的图象上方是不可能的;
的图象上方是不可能的;
(2)如图2,当![]() 时,即
时,即![]() ,对于
,对于![]() 的函数
的函数![]() 的图象恒在
的图象恒在![]() 的图象上方;
的图象上方;
(3)如图3,当![]() 时,即
时,即![]() ,函数
,函数![]() 为过坐标原点且开口向上的二次函数,要使
为过坐标原点且开口向上的二次函数,要使![]() 的函数
的函数![]() 的图象恒在
的图象恒在![]() 的图象上方,只需函数
的图象上方,只需函数![]() 的图象与
的图象与![]() 轴的交点不在
轴的交点不在![]() 的右边,即
的右边,即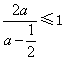 ,则
,则![]() ,且
,且![]() ,即
,即![]() .
.
综上可知当![]() 时,对
时,对![]() 的函数
的函数![]() 的图象恒在
的图象恒在![]() 的图象上方,即当
的图象上方,即当![]() 时函数
时函数![]() 的图象恒在直线
的图象恒在直线![]() 的下方。
的下方。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,点
,点