题目内容
在△ABC中,已知sinA+sinC=2sinB,且∠B=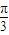 ,若△ABC的面积为
,若△ABC的面积为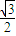 ,则∠B的对边b等于( )
,则∠B的对边b等于( )A.1
B.
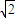
C.
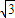
D.
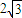
【答案】分析:利用三角形的面积公式表示出三角形ABC的面积,把已知的面积及sinB的值代入,求出ac的值,再利用正弦定理化简已知的等式得到a+c=2b,同时利用余弦定理表示出b2=a2+c2-2accosB,利用完全平方公式变形后,将a+c,ac及cosB的值代入,得到关于b的方程,求出方程的解即可得到b的值.
解答:解:∵△ABC的面积S= acsinB=
acsinB=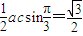 ,
,
∴ac=2,
又根据正弦定理化简sinA+sinC=2sinB得:a+c=2b,
∴由余弦定理: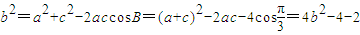 ,
,
∴3b2=6,即b2=2,
∴b=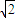 .
.
故选B
点评:此题属于解三角形的题型,涉及的知识有:三角形的面积公式,正弦、余弦定理,以及完全平方公式的运用,熟练掌握公式及定理是解本题的关键.
解答:解:∵△ABC的面积S=
 acsinB=
acsinB=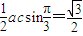 ,
,∴ac=2,
又根据正弦定理化简sinA+sinC=2sinB得:a+c=2b,
∴由余弦定理:
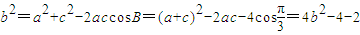 ,
,∴3b2=6,即b2=2,
∴b=
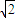 .
.故选B
点评:此题属于解三角形的题型,涉及的知识有:三角形的面积公式,正弦、余弦定理,以及完全平方公式的运用,熟练掌握公式及定理是解本题的关键.

练习册系列答案
相关题目
在△ABC中,已知|
|=4,|
|=1,S△ABC=
,则
•
的值为( )
| AB |
| AC |
| 3 |
| AB |
| AC |
| A、-2 | B、2 | C、±4 | D、±2 |