题目内容
18.求值(或化简).(1)$\root{4}{81×\sqrt{{9}^{\frac{2}{3}}}}$;
(2)2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$;
(3)0.0001${\;}^{-\frac{1}{4}}$+27${\;}^{\frac{2}{3}}$-($\frac{49}{64}$)${\;}^{-\frac{1}{2}}$+($\frac{1}{9}$)-1.5.
分析 利用公式${a}^{\frac{m}{n}=\root{n}{{a}^{m}}}$,结合分数指数幂的性质和运算法则求解.
解答 解:(1)$\root{4}{81×\sqrt{{9}^{\frac{2}{3}}}}$=$8{1}^{\frac{1}{4}}×{9}^{\frac{1}{12}}$=3×${3}^{\frac{1}{6}}$=${3}^{\frac{7}{6}}$.
(2)2$\sqrt{3}$×$\root{3}{1.5}$×$\root{6}{12}$=$2×{3}^{\frac{1}{2}}×\frac{{3}^{\frac{1}{3}}}{{2}^{\frac{1}{3}}}×{3}^{\frac{1}{6}}×{2}^{\frac{1}{3}}$=2×3=6.
(3)0.0001${\;}^{-\frac{1}{4}}$+27${\;}^{\frac{2}{3}}$-($\frac{49}{64}$)${\;}^{-\frac{1}{2}}$+($\frac{1}{9}$)-1.5
=(10-4)${\;}^{-\frac{1}{4}}$+(33)${\;}^{\frac{2}{3}}$-[($\frac{7}{8}$)2]${\;}^{-\frac{1}{2}}$+[($\frac{1}{3}$)2]${\;}^{-\frac{3}{2}}$
=10+9-$\frac{8}{7}$+27
=$\frac{314}{7}$.
点评 本题考查有理数指数幂的化简求值,是基础题,解题时要认真审题,注意分数指数幂的性质和运算法则的合理运用.

练习册系列答案
相关题目
8.已知函数f(x)=2sin(π+x)sin(x+$\frac{π}{3}$+φ)的图象关于原点对称,其中φ∈(0,π),则函数g(x)=cos(2x-φ)的图象.( )
| A. | 关于点($\frac{π}{12},0$)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(-x)的图象向右平移$\frac{π}{12}$个单位得到 |
3.已知a2>b>a>1,则logb$\frac{b}{a}$,logba,logab的大小关系是( )
| A. | logba<logab<logb$\frac{b}{a}$ | B. | logb$\frac{b}{a}$<logba<logab | ||
| C. | logba<logb$\frac{b}{a}$<logab | D. | logab<logb$\frac{b}{a}$<logba |
10.(1+x)+(1+x)2+…+(1+x)n的所有二项式的各项系数和是( )
| A. | 2n+1 | B. | 2n+1+1 | C. | 2n+1-1 | D. | 2n+1-2 |
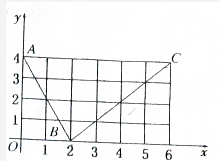 如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4).
如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4). 程序框图,如图所示,当箭头a指向①时输出S的值为m,当箭头a指向②时,输出S的值为n,则m+n=20.
程序框图,如图所示,当箭头a指向①时输出S的值为m,当箭头a指向②时,输出S的值为n,则m+n=20.