题目内容
已知函数 ,若
,若 ,则
,则 的值为
的值为
 ,若
,若 ,则
,则 的值为
的值为 A. | B. | C.1 | D.与 和 和 有关 有关 |
A
利用已知条件求得sin(2α+φ)=1,cos (2α+φ)=0,化简f(α+ ) 等于2sin[2α+φ)+
) 等于2sin[2α+φ)+ ],
],
利用两角和的正弦公式展开运算.
解:∵函数f(x)=2sin(2x+φ),若f(α)=2,∴2=2sin(2α+φ),∴sin(2α+φ)=1,
∴cos (2α+φ)=0,则f(α+ )=2sin[2(α+
)=2sin[2(α+ )+φ]="2sin" (2α+φ+
)+φ]="2sin" (2α+φ+ )
)
=2[sin(2α+φ)cos +cos(2α+φ)sin
+cos(2α+φ)sin ]=2[1×
]=2[1× .
.
故选 A.
 ) 等于2sin[2α+φ)+
) 等于2sin[2α+φ)+ ],
],利用两角和的正弦公式展开运算.
解:∵函数f(x)=2sin(2x+φ),若f(α)=2,∴2=2sin(2α+φ),∴sin(2α+φ)=1,
∴cos (2α+φ)=0,则f(α+
 )=2sin[2(α+
)=2sin[2(α+ )+φ]="2sin" (2α+φ+
)+φ]="2sin" (2α+φ+ )
) =2[sin(2α+φ)cos
 +cos(2α+φ)sin
+cos(2α+φ)sin ]=2[1×
]=2[1× .
. 故选 A.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
 ,
, ,
,
 时,求函数
时,求函数 的最大值;
的最大值; ,且
,且 在
在 的取值范围.
的取值范围. ·
· =
= ·
· 。
。 ,
,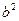 ,
, 成等差数列;
成等差数列; B及sinB+cosB的取值范围
B及sinB+cosB的取值范围
 的值;
的值;
 .
.  ,求
,求 ;
; ,求
,求 的取值范围.
的取值范围. 图象是由函数
图象是由函数 的图象按如下变换所得
的图象按如下变换所得

 右移
右移 的图像向左平移
的图像向左平移 个单位,再向上平移1个单位,所得图像的函数解析式( )
个单位,再向上平移1个单位,所得图像的函数解析式( ) .y=
.y= B.y=
B.y= C.y=1+
C.y=1+ D.y=
D.y=
 ,则
,则 等于( )
等于( )




 ,移动am后到达B点,又测得塔底C点的仰角为
,移动am后到达B点,又测得塔底C点的仰角为 ,测得塔尖D点的仰角为
,测得塔尖D点的仰角为 ,求塔高CD
,求塔高CD