题目内容
已知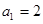 ,点
,点 在函数
在函数 的图像上,(其中
的图像上,(其中 )
)
(Ⅰ)求证数列 是等比数列;
是等比数列;
(Ⅱ)设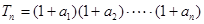 ,求
,求 及数列
及数列 的通项.
的通项.
【答案】
(Ⅰ)详见解析;(Ⅱ)

【解析】
试题分析:(Ⅰ)首先由已知条件得数列 的递推关系,根据要证的目标,必须把递推关系变形为
的递推关系,根据要证的目标,必须把递推关系变形为 和
和 的关系,两边取对数即证.
的关系,两边取对数即证.
(Ⅱ)根据(Ⅰ)的结果求出数列 的通项公式,进而求出数列
的通项公式,进而求出数列 的通项公式,
的通项公式,
然后求出 和
和 .
.
试题解析:(Ⅰ) 点
点 在函数
在函数 的图像上,
的图像上,
 ,
, ,
, ,两边取对数得:
,两边取对数得:
 即
即 ,
,
所以数列 是公比为2的等比数列.
是公比为2的等比数列.
(Ⅱ)由(Ⅰ)知 ,
,

考点:1.等比数列的判断与证明; 2.等比数列求和.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
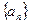 中,已知点
中,已知点 在
在 函数
函数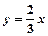 的图像上,且
的图像上,且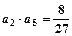 .
.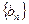 的前
的前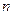 项和为
项和为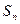 ,且
,且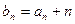 ,求
,求 在函数
在函数 的图像上 , 则下列点中不可能在此图像上的是( )
的图像上 , 则下列点中不可能在此图像上的是( ) B.
B. C.
C.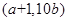 D.
D.