题目内容
 如图所示,棱长都相等的棱锥A-BCD中,E、F分别在棱AB、CD上,使
如图所示,棱长都相等的棱锥A-BCD中,E、F分别在棱AB、CD上,使| AE |
| EB |
| CF |
| FD |
| A、f(λ)在(0,+∞)上单调递增 |
| B、f(λ)在(0,+∞)上单调递减 |
| C、f(λ)在(0,1)上单调递增,而在(1,+∞)上单调递减 |
| D、f(λ)在(0,+∞)上为常数 |
分析:取BC的中点M,连接EM,MF,根据异面直线所成角的定义可知∠MEF表示EF与AC所成的角的度数,∠MFE表示EF与BD所成角的度数,而异面直线AC与BD的所成角为∠EMF是定值,则αλ+βλ=π-∠EMF为定值,从而得到结论.
解答:解:取BC的中点M,连接EM,MF
αλ表示EF与AC所成的角的度数即αλ=∠MEF,
βλ表示EF与BD所成角的度数即为βλ=∠MFE,
∵异面直线AC与BD的所成角为∠EMF是定值
∴αλ+βλ=π-∠EMF为定值
∴f(λ)在(0,+∞)上为常数
故选:D
αλ表示EF与AC所成的角的度数即αλ=∠MEF,
βλ表示EF与BD所成角的度数即为βλ=∠MFE,
∵异面直线AC与BD的所成角为∠EMF是定值
∴αλ+βλ=π-∠EMF为定值
∴f(λ)在(0,+∞)上为常数
故选:D
点评:本题主要考查了异面直线及其所成角,同时考查推理论证的能力,转化与划归的思想,属于中档题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
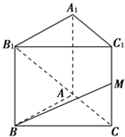 如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是
如图所示,已知正三棱柱ABC-A1B1C1的各条棱长都相等,M是侧棱CC1的中点,则异面直线AB1和BM所成的角的大小是 (2013•山东)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( )
(2013•山东)一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示该四棱锥侧面积和体积分别是( ) 如图所示,棱长都相等的棱锥A-BCD中,E、F分别在棱AB、CD上,使
如图所示,棱长都相等的棱锥A-BCD中,E、F分别在棱AB、CD上,使 (λ>0)设f(λ)=αλ+βλ,αλ表示EF与AC所成的角的度数,βλ表示EF与BD所成角的度数,则
(λ>0)设f(λ)=αλ+βλ,αλ表示EF与AC所成的角的度数,βλ表示EF与BD所成角的度数,则