Question

（2012•珠海二模）如图，长方体ABCD-A₁B₁C₁D₁中，CC₁=4，AB=BC=3．
（1）若E、F分别是BC₁、A₁C₁中点，求证：EF∥平面DCC₁；
（2）求二面角A₁-BC₁-D的正弦值．

Answer 1

分析：（I）连接D₁B₁，B₁C，利用长方体的性质可得E、F分别是B₁D₁和B₁C的中点，再利用三角形的中位线定理可得EF∥D₁C．利用线面平行的判定定理即可证明；
（II）通过建立空间直角坐标系，利用两个平面的法向量的夹角即可得到二面角．

解答：（Ⅰ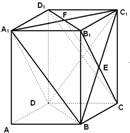）证明：连接D₁B₁，B₁C，则长方体ABCD-A₁B₁C₁D₁中，BC₁∩B₁C=E，D₁B₁∩A₁C₁=F，
∴E、F分别是B₁D₁和B₁C的中点
∴EF∥D₁C．又EF?平面DCC₁；D₁C?平面DCC₁；
∴EF∥平面DCC₁；
（Ⅱ）解：建立如图所示的空间直角坐标系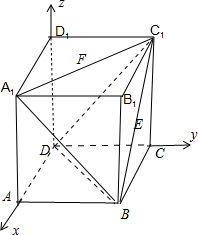，则D（0，0，0），B（3，3，0），C₁（0，3，4），A₁（3，0，4）．
∴

BC1

=（-3，0，4），

DB

=（3，3，0），

A1C1

=（-3，3，0）．
设平面DBC₁的法向量为

n1

=(x1，y1，z1)，则

n1 • DB =3x1+3y1=0 n1 • BC1 =-3x1+4z1=0

，取x₁=4，解得y₁=-4，z₁=3，∴

n1

=（4，-4，3）；
设平面A₁BC₁的法向量为

n2

=（x₂，y₂，z₂），则

n2 • BC1 =-3x2+4z2=0 n2 • A1C1 =-3x2+3y2=0

，取x₂=4，解得y₂=4，z₂=3，∴

n2

=（4，4，3）；
∴cos＜

n1

，

n2

＞=

n1 • n2

| n1 | | n2 |

=

9

41

，
设二面角A₁-BC₁-D的大小为θ，则sinθ=

1-( 9 41 )2

=

40

41

．
即二面角A₁-BC₁-D的正弦值为

40

41

．

点评：本题综合考查了长方体的性质、三角形的中位线定理、线面平行的判定定理、通过距离空间直角坐标系利用法向量的夹角求二面角等基础知识与基本技能，考查了空间想象能力、推理能力和计算能力．