题目内容
用数学归纳法证明：对任意n∈N＋，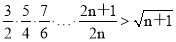
成立．
见解析
【解析】(1)当n＝1时，左边＝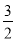
，右边＝
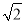，因为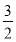
>
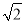，所以不等式成立．
(2)假设当n＝k时不等式成立，即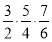
……
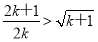成立，则当n＝k＋1时，左边＝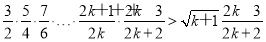
＝
?＝
.?
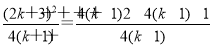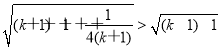所以当n＝k＋1时，不等式也成立，由(1)，(2)可得不等式恒成立．
练习册系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
暑假接力赛新疆青少年出版社系列答案题目内容
用数学归纳法证明：对任意n∈N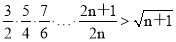＋，成立．
见解析
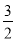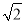【解析】(1)当n＝1时，左边＝，右边＝，因为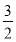>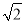，所以不等式成立．
(2)假设当n＝k时不等式成立，即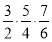……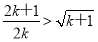成立，则当n＝k＋1时，左边＝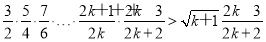
＝?＝.?
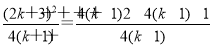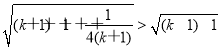所以当n＝k＋1时，不等式也成立，由(1)，(2)可得不等式恒成立．
暑假接力赛新疆青少年出版社系列答案
