Question

正三角形的一个顶点位于坐标原点,另外两个顶点在抛物线y²=2px(p＞0)上,求这个三角形的边长.

Answer 1

分析:由于正三角形与抛物线都是轴对称,可以证明A、B两点关于x轴对称,进而求出|AB|的长.

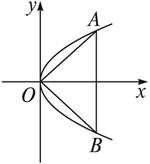
解:如图,设正三角形OAB的顶点A、B在抛物线上,且坐标分别为(x₁,y₁),(x₂,y₂),y₁²=2px₁,y₂²=2px₂,

又∵|OA|=|OB|,∴x₁²+y₁²=x₂²+y₂²,即x₁²-x₂²+2px-2px₂=0.∴(x₁-x₂)·(x₁+x₂+2p)=0.

∵x₁＞0,x₂＞0,2p＞0,∴x₁+x₂+2p≠0,即A、B两点关于x轴对称,则∠AOx=30°.

∴AB⊥x轴.∴y₁=x₁tan30°=x₁.又∵x₁=,∴y₁=2p.

而|AB|=2y₁=4p即为所求边长.

点评:本题的关键是根据抛物线的对称性和正三角形的性质证明A、B两点关于x轴对称,解答本题要注意不能只凭主观判断而忽视了推理证明的过程.