题目内容
抛物线 绕
绕 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .
 绕
绕 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .8
试题分析:根据旋转体的对称性,不妨设正方体的一个对角面恰好在
 平面内,组合体被此面所截得的截面图如下:
平面内,组合体被此面所截得的截面图如下:
设正方体的棱长为
 ,则
,则 ,
, ,
,因为
 ,所以,
,所以, ,即:
,即:
解得:
 或
或 ,因为
,因为 ,所以
,所以 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 过点
过点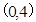 ,离心率为
,离心率为 .
. 的方程;
的方程; 且斜率为
且斜率为 的直线被椭圆所截得线段的中点坐标.
的直线被椭圆所截得线段的中点坐标. :
: ,直线
,直线 交椭圆
交椭圆 两点.
两点.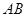 为直径的圆的方程.
为直径的圆的方程.  是抛物线
是抛物线 上的两个点,点
上的两个点,点 的坐标为
的坐标为 ,直线
,直线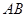 的斜率为
的斜率为 .设抛物线
.设抛物线 的焦点在直线
的焦点在直线 ,过
,过 两点分别作W的切线,记两切线的交点为
两点分别作W的切线,记两切线的交点为 . 判断四边形
. 判断四边形 是否为梯形,并说明理由.
是否为梯形,并说明理由. ,椭圆
,椭圆 以
以 的长轴为短轴,且与
的长轴为短轴,且与 ,求直线
,求直线 的方程.
的方程.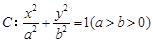 的离心率为
的离心率为 ,其中左焦点
,其中左焦点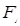 (-2,0).
(-2,0). 上一点P到y轴的距离为6,则点P到焦点的距离为( )
上一点P到y轴的距离为6,则点P到焦点的距离为( ) 中,
中, 为侧面
为侧面 所在平面上的一个动点,且
所在平面上的一个动点,且 的距离是
的距离是 距离的
距离的 倍,则动点
倍,则动点 的圆心为抛物线
的圆心为抛物线 的焦点,直线
的焦点,直线 与圆
与圆 相切,则该圆的方程为( )
相切,则该圆的方程为( )


