Question

过双曲线

x2

3

-y2=1的右焦点F₂，作倾斜角为

π

4

的直线交双曲线于A、B两点，
求：（1）|AB|的值；
（2）△F₁AB的周长（F₁为双曲线的左焦点）．

Answer 1

分析：（1）由双曲线方程

x2

3

-y2=1可得a=

3

，b=1，又由c²=a²+b²，得c=2，F₂（2，0），故直线方程为y=x-2，再由弦长公式能够导出|AB|的值．
（2）由双曲线定义得|AF₁|=|AF₂|+2a，|BF₁|=|BF₂|+2a，由此能求出△F₁AB的周长．

解答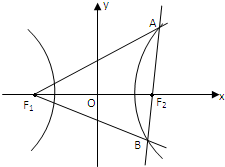：解：（1）由双曲线方程

x2

3

-y2=1可得a=

3

，b=1，
又由c²=a²+b²，得c=2，F₂（2，0）

所以直线AB的方程为：y=x-2 设A(x1，y1)、B(x2，y2) 由 y=x-2 x2 3 -y2=1 消去y得2x2-12x+15=0 ∴x1+x2=6，x1x2= 15 2 由弦长公式|AB|= 1+k2 • (x1+x2)2-4x1x2 ，得 |AB|= 1+12 • 62-4× 15 2 =2 3

（2）如图，由双曲线定义得：
|AF₁|=|AF₂|+2a，
|BF₁|=|BF₂|+2a
∴△F₁AB的周长=|AF₁|+|BF₁|+|AB|
=|AF₁|+|BF₂|+4×

3

+|AB|
=2|AB|+4

3

=8

3

点评：本题考查直线的圆锥曲线的位置关系，解题时要注意弦长公式的运用，合理地运用数形结合思想解题．