题目内容
11．定义关于x的不等式|x-A|＜B（A∈R，B＞0）的解集称为A的B邻域．若a+b-3的a+b邻域是区间（-3，3），则a2+b2的最小值是$\frac{9}{2}$．分析 根据新定义由题意得：|x-（a+b-3）|＜a+b的解集为区间（-3，3），从而得到关于 a，b的等量关系，再利用基本不等式求得a2+b2的最小值．
解答 解：由题意可得|x-（a+b-3）|＜a+b的解集为（-3，3），|x-（a+b-3）|＜a+b等价于（-3，2（a+b）-3），
∴2（a+b）-3=3，求得a+b=3，∴a2+b2≥$\frac{{（a+b）}^{2}}{2}$=$\frac{9}{2}$，
故a2+b2的最小值为$\frac{9}{2}$，
故答案为：$\frac{9}{2}$．
点评 本小题主要考查绝对值不等式的解法、基本不等式等基础知识，考查运算求解能力与化归与转化思想，属于基础题．
练习册系列答案
轻松暑假总复习系列答案
相关题目
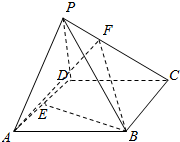如图所示，P为?ABCD所在平面外一点，E为AD的中点，F为PC上一点，当PA∥平面EBF时，$\frac{PF}{FC}$=$\frac{1}{2}$．
我校为进行“阳光运动一小时”活动，计划在一块直角三角形ABC的空地上修建一个占地面积为S（平方米）的矩形AMPN健身场地．如图，点M在AC上，点N在AB上，且P点在斜边BC上．已知∠ACB=60°，|AC|=30米，|AM|=x米，x∈[10，20]．设矩形AMPN健身场地每平方米的造价为$\frac{37k}{{\sqrt{S}}}$元，再把矩形AMPN以外（阴影部分）铺上草坪，每平方米的造价为$\frac{12k}{{\sqrt{S}}}$元（k为正常数）．