题目内容
若(9,a)在函数y=log2x的图象上,则有关函数f(x)=ax+a-x性质的描述,正确提
- A.它是定义域为R的奇函数
- B.它在定义域R上有4个单调区间
- C.它的值域为(0,+∞)
- D.函数y=f(x-2)的图象关于直线x=2对称
A
分析:求出a的值并确定范围后结合a的取值范围判断f(x)的奇偶性和对称性,结合双曲函数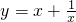 的性质给出值域、单调性.
的性质给出值域、单调性.
解答:显然定义域为R,由题知a=log29>3,令t=ax,则t>0.
借助于双曲函数y=t+ ,可得函数f(x)的值域为[2,+∞).
,可得函数f(x)的值域为[2,+∞).
函数f(x)为奇函数、图象关于原点对称,函数y=f(x-2)的图象关于点(2,0)对称.
结合所给的选项,
故选 A.
点评:该题基本初等函数I中一道很好的综合题,是选择题中难度较大的题目,对双曲函数 的
的
图象与性质有较高的要求,解答本题也可以利用排除法解答,属于中档题.
分析:求出a的值并确定范围后结合a的取值范围判断f(x)的奇偶性和对称性,结合双曲函数
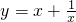 的性质给出值域、单调性.
的性质给出值域、单调性.解答:显然定义域为R,由题知a=log29>3,令t=ax,则t>0.
借助于双曲函数y=t+
 ,可得函数f(x)的值域为[2,+∞).
,可得函数f(x)的值域为[2,+∞).函数f(x)为奇函数、图象关于原点对称,函数y=f(x-2)的图象关于点(2,0)对称.
结合所给的选项,
故选 A.
点评:该题基本初等函数I中一道很好的综合题,是选择题中难度较大的题目,对双曲函数
 的
的图象与性质有较高的要求,解答本题也可以利用排除法解答,属于中档题.

练习册系列答案
相关题目
 的值为( )
的值为( )