题目内容
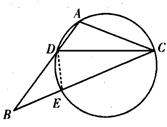
如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交于BC于点E,AB=2AC.
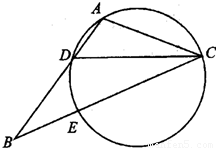
(Ⅰ)求证:BE=2AD;
(Ⅱ)当AC=1,EC=2时,求AD的长.
【答案】
(Ⅰ)详见解析;(Ⅱ)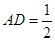 .
.
【解析】
试题分析:(Ⅰ)要证明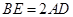 ,注意到
,注意到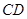 是
是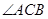 的平分线,等角对等弦,可连接
的平分线,等角对等弦,可连接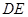 ,则
,则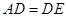 ,可证
,可证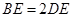 ,又因为
,又因为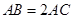 ,可证
,可证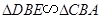 即可, 由圆内接四边形的性质可证;(Ⅱ)根据割线定理,建立
即可, 由圆内接四边形的性质可证;(Ⅱ)根据割线定理,建立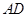 的方程,解出
的方程,解出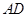 即可.
即可.
试题解析:(Ⅰ)连接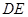 ,因为
,因为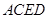 是圆的内接四边形,所以
是圆的内接四边形,所以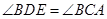 ,又
,又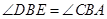 ,所以
,所以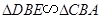 ,即有
,即有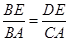 ,又
,又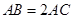 ,所以
,所以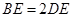 ,又
,又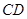 是
是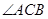 的平分线,
的平分线,
所以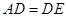 ,从而
,从而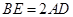 .
.
(Ⅱ)由条件的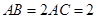 设
设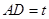 ,根据割线定理得
,根据割线定理得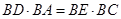 ,即
,即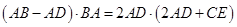 ,所以
,所以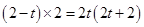 即
即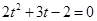
解得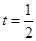 ,或
,或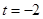 (舍去),即
(舍去),即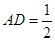
考点:本小题考查割线定理,相似三角形,等角对等弦,圆内接四边形,考查分析问题、解决问题的能力,及推理论证能力.

练习册系列答案
 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
 如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=
如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm,
如图,在△ABC中,已知∠ABC=90°,AB上一点E,以BE为直径的⊙O恰与AC相切于点D,若AE=2cm, 如图,在△ABC中,设
如图,在△ABC中,设 如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3.
如图,在△ABC中,∠B=45°,D是BC边上的一点,AD=5,AC=7,DC=3. 如图,在△ABC中,已知
如图,在△ABC中,已知