Question

已知点A(-3,0),B(3,0),P为圆(x+3)²+y²=24上一动点，线段PB的中垂线交直线PA于点Q.

(1)求点Q的轨迹方程;

(2)过点C(2,0)作直线交点Q的轨迹于M、N两不同的点,且=λ,M关于x轴对称点为E.求证:=λ.

Answer 1

(1)解:∵|AB|＞|AP|,∴线段BP中垂线交PA延长线于点Q,如图(1);或交AP延长线于点Q,如图(2).

∴|QB|-|QA|=2或-2.

       

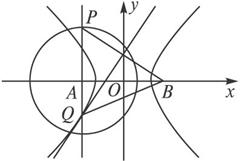
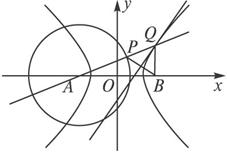
(1)                                             (2)

∴Q的轨迹是以A、B为焦点,实轴长为2的双曲线.

∴点Q的轨迹方程为=1.

(2)证明:设M(x₁,y₁),N(x₂,y₂)，则E(x₁,-y₁).∴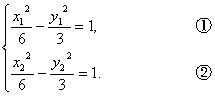

由=λ,得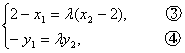

①-②×λ²得=1-λ²,        ⑤

③⑤联立可得x₁=,x₂=,

∴3-x₁=,3-x₂=.∴3-x₁=λ(3-x₂).又y₁=-λy₂,∴=λ.