题目内容
计算下列各式:(Ⅰ)(lg2)2+lg5•lg20-1;
(Ⅱ)
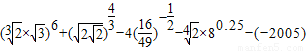 .
.
【答案】分析:(Ⅰ)利用对数的运算性质,把(lg2)2+lg5•lg20-1等价转化为lg22+(1-lg2)(1+lg2)-1,由此能够求出结果.
(Ⅱ)利用有理数指数幂的运算性质,把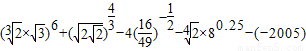 等价转化
等价转化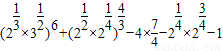 ,由此能求出结果.
,由此能求出结果.
解答:解:(Ⅰ)(lg2)2+lg5•lg20-1
=lg22+(1-lg2)(1+lg2)-1
=lg22+1-lg22-1=0.
(Ⅱ)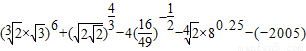
=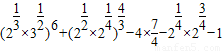
=22×33+2-7-2-1
=100.
点评:本题考查对数的运算性质和有理数指数幂的运算性质,是基础题.解题时要认真审题,仔细解答.
(Ⅱ)利用有理数指数幂的运算性质,把
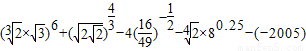 等价转化
等价转化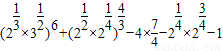 ,由此能求出结果.
,由此能求出结果.解答:解:(Ⅰ)(lg2)2+lg5•lg20-1
=lg22+(1-lg2)(1+lg2)-1
=lg22+1-lg22-1=0.
(Ⅱ)
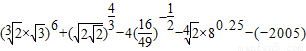
=
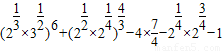
=22×33+2-7-2-1
=100.
点评:本题考查对数的运算性质和有理数指数幂的运算性质,是基础题.解题时要认真审题,仔细解答.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目