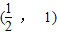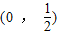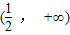题目内容
若定义域在区间(-1,0)内的函数f(x)=log2a(x+1),(a>0且a≠
)满足f(x)>0,则a的取值范围是( )
| 1 | 2 |
分析:由x的范围求出对数真数的范围,再根据对数值的符号,判断出底数的范围,列出不等式进行求解.
解答:解:∵x∈(-1,0)
∴x+1∈(0,1)
由f(x)>0得,
∴log2a(x+1)>0
∴0<2a<1
∴0<a<
.
故选C.
∴x+1∈(0,1)
由f(x)>0得,
∴log2a(x+1)>0
∴0<2a<1
∴0<a<
| 1 |
| 2 |
故选C.
点评:本题考查对数函数的图象和对数函数的单调性与特殊点,解答关键是利用对数函数的性质,属基本题型的考查.

练习册系列答案
相关题目
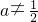 )满足f(x)>0,则a的取值范围是
)满足f(x)>0,则a的取值范围是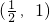
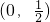
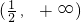
 )满足f(x)>0,则a的取值范围是( )
)满足f(x)>0,则a的取值范围是( )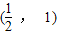
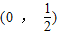
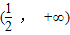
 )满足f(x)>0,则a的取值范围是( )
)满足f(x)>0,则a的取值范围是( )