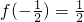题目内容
定义:符号[x]表示不超过实数x的最大整数,如[3.8]=3,[-2.3]=-3,,等,设函数f(x)=x-[x],则下列结论中不正确的是( )A.

B.f(x+y)=f(x)+f(y)
C.f(x+1)=f(x)
D.0≤f(x)<1
【答案】分析:符号[x]表示不超过实数x的最大整数,函数f(x)=x-[x],知f(- )=
)= =-
=- =
= .f(x+y)=x+y-[x+y]≠f(x)+f(y)=x+y-[x]-[y];f(x+1)=x+1-[x+1]=f(x)=x-[x];f(x+1)=f(x).
.f(x+y)=x+y-[x+y]≠f(x)+f(y)=x+y-[x]-[y];f(x+1)=x+1-[x+1]=f(x)=x-[x];f(x+1)=f(x).
解答:解:∵符号[x]表示不超过实数x的最大整数,
函数f(x)=x-[x],
∴f(- )=
)= =-
=- =
= ,故A成立.
,故A成立.
∵f(x+y)=x+y-[x+y],
f(x)+f(y)=x+y-[x]-[y],
∴f(x+y)≠f(x)+f(y).故B不成立.
∵f(x+1)=x+1-[x+1],f(x)=x-[x],
∴f(x+1)=f(x),故C成立;
0≤f(x)<1,故D成立.
故选B.
点评:本题考查函数解析式的求解和常用方法,解题时要认真审题,仔细解答,注意新定义的灵活运用.
 )=
)= =-
=- =
= .f(x+y)=x+y-[x+y]≠f(x)+f(y)=x+y-[x]-[y];f(x+1)=x+1-[x+1]=f(x)=x-[x];f(x+1)=f(x).
.f(x+y)=x+y-[x+y]≠f(x)+f(y)=x+y-[x]-[y];f(x+1)=x+1-[x+1]=f(x)=x-[x];f(x+1)=f(x).解答:解:∵符号[x]表示不超过实数x的最大整数,
函数f(x)=x-[x],
∴f(-
 )=
)= =-
=- =
= ,故A成立.
,故A成立.∵f(x+y)=x+y-[x+y],
f(x)+f(y)=x+y-[x]-[y],
∴f(x+y)≠f(x)+f(y).故B不成立.
∵f(x+1)=x+1-[x+1],f(x)=x-[x],
∴f(x+1)=f(x),故C成立;
0≤f(x)<1,故D成立.
故选B.
点评:本题考查函数解析式的求解和常用方法,解题时要认真审题,仔细解答,注意新定义的灵活运用.

练习册系列答案
相关题目