题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,若存在
时,若存在![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 为正整数,方程
为正整数,方程![]() 的两个实数根
的两个实数根![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() 或
或![]() ;(2)11.
;(2)11.
【解析】试题分析:(1)存在![]() ,使得
,使得![]() 等价于
等价于![]() 在
在![]() 上有两个不等实根,或
上有两个不等实根,或![]() 在
在![]() 上有两个不等实根,结合二次函数的顶点在直线下方或上方列不等式组求解即可;(2)利用一元二次方程方程根的分别,列不等式组,根据
上有两个不等实根,结合二次函数的顶点在直线下方或上方列不等式组求解即可;(2)利用一元二次方程方程根的分别,列不等式组,根据![]() 为正整数,先初步判断
为正整数,先初步判断![]() 的范围,再利用分类讨论思想求解即可.
的范围,再利用分类讨论思想求解即可.
试题解析:(1)当![]() 时,
时, ![]()
由题意可知, ![]() 在
在![]() 上有两个不等实根,或
上有两个不等实根,或![]() 在
在![]() 上有两个不等实根,则
上有两个不等实根,则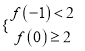 或
或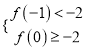 ,
,
解得![]() 或
或![]()
即实数![]() 的取值范围是
的取值范围是![]() 或
或![]() .
.
(2)设![]() ,则由题意得
,则由题意得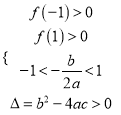 ,即
,即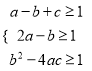 ,
,
所以![]() ,由于
,由于![]()
①当![]() 时,
时, ![]() ,且
,且![]() 无解,
无解,
②当![]() 时,
时, ![]() ,且
,且![]() ,于是
,于是![]() 无解,
无解,
③当![]() 时,
时, ![]() ,且
,且![]() ,由
,由![]() ,得
,得![]() ,此时有解
,此时有解![]() ,
,
综上所述, ![]() ,当
,当![]() 时取等号,即
时取等号,即![]() 的最小值为11.
的最小值为11.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目