题目内容
设直线L的斜率k=2，P1（3，5），P2（x2，7），P（-1，y3） 是直线L上的三点，则x2，y3的值依次是（ ）
分析：先求直线L的方程，再将P2（x2，7），P（-1，y3）代入，我们就可以求出x2，y3的值
解答：解：∵直线L的斜率k=2，P1（3，5），
∴过P1的直线方程L为：y-5=2（x-3），即2x-y-1=0
∵P2（x2，7），P（-1，y3） 是直线L上的点，
∴2x2-7-1=0，2×（-1）-y3-1=0
∴x2=4，y3=-3
故选D．
∴过P1的直线方程L为：y-5=2（x-3），即2x-y-1=0
∵P2（x2，7），P（-1，y3） 是直线L上的点，
∴2x2-7-1=0，2×（-1）-y3-1=0
∴x2=4，y3=-3
故选D．
点评：已知点与斜率，利用点斜式可求方程，利用点在直线上，将点代入直线方程，体现了方程与曲线的联系．
练习册系列答案
名校课堂系列答案
相关题目
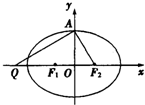（2012•河南模拟）设椭圆