题目内容
(12分)若函数y＝lg(3－4x＋x2)的定义域为M，.当x∈M时，
求f(x)＝2x＋2－3×4x的最值及相应的x的值．
【答案】
解 ∵y＝lg(3－4x＋x2)，∴3－4x＋x2>0，
解得x<1或x>3，∴M＝{x|x<1，或x>3}，
f(x)＝2x＋2－3×4x＝4×2x－3×(2x)2.
令2x＝t，∵x<1或x>3，
∴t>8或0<t<2.
f(t)＝4t－3t2＝－32＋(t>8或0<t<2)．
由二次函数性质可知：
当0<t<2时，f(t)∈，
当t>8时，f(x)∈(－∞，－160)，
当2x＝t＝，即x＝log2时，f(x)max＝.
综上可知：当x＝log2时，f(x)取到最大值为，无最小值
【解析】略
练习册系列答案
考前必练系列答案
相关题目
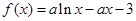（a∈R且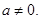
）． 
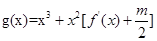在区间(t，3)上总不是单调函数，求m的取值范围.
，
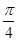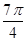]上的简图；
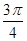]上的单调递增区间；试问：当x在R上取何值