题目内容
(本小题满分12分)已知函数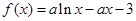 (a∈R且
(a∈R且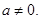 ).
).
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意t∈[1,2],函数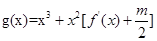 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围.
【答案】
(1) 当a>0时, 的单调增区间为(0,1),单调减区间为(1,+∞)
的单调增区间为(0,1),单调减区间为(1,+∞)
当a<0时, 的单调增区间为(1,+∞),单调减区间为(0,1)
的单调增区间为(1,+∞),单调减区间为(0,1)
(2)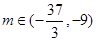
【解析】
试题分析:解:(本小题满分12分)
(1)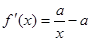 =
=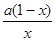 . ∵x>0, ………………………1分
. ∵x>0, ………………………1分
当a>0时, 的单调增区间为(0,1),单调减区间为(1,+∞)……………2分
的单调增区间为(0,1),单调减区间为(1,+∞)……………2分
当a<0时, 的单调增区间为(1,+∞),单调减区间为(0,1).……………4分
的单调增区间为(1,+∞),单调减区间为(0,1).……………4分
(2)∵函数y= 在点(2,
在点(2,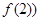 处的切线斜率为1,
处的切线斜率为1,
∴ , 解得a=-2.………………………………5分
, 解得a=-2.………………………………5分
∴ , ∴
, ∴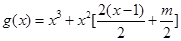
 .
.
∴ .……………………………7分
.……………………………7分
令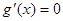 ,即
,即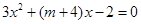 , ∵△=
, ∵△=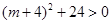 ,
,
∴方程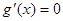 有两个实根且两根一正一负,即有且只有一个正根.…………8分
有两个实根且两根一正一负,即有且只有一个正根.…………8分
∵函数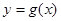 在区间(t,3)(其中t∈[1,2])上总不是单调函数,
在区间(t,3)(其中t∈[1,2])上总不是单调函数,
∴方程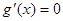 在
在 上有且只有一个实数根.………………………9分
上有且只有一个实数根.………………………9分
又∵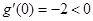 ,∴
,∴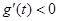 ,
, .
.
∴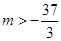 ,且
,且 .…………………………………………10分
.…………………………………………10分
∵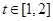 ,∴
,∴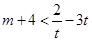 ,
,
令 ,则
,则 ,即
,即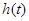 在
在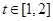 上单调递减.
上单调递减.
∴ ,即
,即 .
.
∴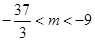 .
.
综上可得,m的取值范围为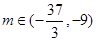 .…………………………………12分
.…………………………………12分
考点:本试题考查了导数的运用
点评:解决该试题的关键是能理解对于导数的符号,运用分类讨论的思想来求解函数的单调性。同时对于函数不单调的处理,可以转换为函数单调时的参数的范围,然后利用补集的思想求解结论,属于中档题。

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目