题目内容
已知两空间向量 =(2,cos θ,sin θ),
=(2,cos θ,sin θ), =(sin θ,2,cos θ),则
=(sin θ,2,cos θ),则 与
与 的夹角为
的夹角为
- A.30°
- B.45°
- C.60°
- D.90°
D
分析:直接求两个向量的数量积,即可求出它们的夹角.
解答:由题意可知: =(2,cos θ,sin θ),
=(2,cos θ,sin θ), =(sin θ,2,cos θ),
=(sin θ,2,cos θ),
所以( )•(
)•( )=
)=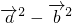 =4+cos2θ+sin2θ-(sin2θ+4+cos2θ)=0,
=4+cos2θ+sin2θ-(sin2θ+4+cos2θ)=0,
所以 与
与 的夹角为90°.
的夹角为90°.
故选D.
点评:本题是基础题,考查向量的数量积的应用,考查计算能力,可以求出 与
与 的坐标表示,然后求两者的数量积.
的坐标表示,然后求两者的数量积.
分析:直接求两个向量的数量积,即可求出它们的夹角.
解答:由题意可知:
 =(2,cos θ,sin θ),
=(2,cos θ,sin θ), =(sin θ,2,cos θ),
=(sin θ,2,cos θ),所以(
 )•(
)•( )=
)=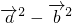 =4+cos2θ+sin2θ-(sin2θ+4+cos2θ)=0,
=4+cos2θ+sin2θ-(sin2θ+4+cos2θ)=0,所以
 与
与 的夹角为90°.
的夹角为90°.故选D.
点评:本题是基础题,考查向量的数量积的应用,考查计算能力,可以求出
 与
与 的坐标表示,然后求两者的数量积.
的坐标表示,然后求两者的数量积. 
练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
已知两空间向量
=(2,cos θ,sin θ),
=(sin θ,2,cos θ),则
+
与
-
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、30° | B、45° |
| C、60° | D、90° |
已知两空间向量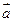 =(2,cos θ,sin θ),
=(2,cos θ,sin θ),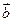 =(sin
=(sin  θ,2,cos θ),则
θ,2,cos θ),则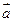 +
+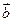 与
与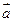 -
-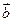 的夹角为( )
的夹角为( )
| A.30° | B.45° | C.60° | D.90° |
 =(2,cos θ,sin θ),
=(2,cos θ,sin θ), =(sinθ,2,cos θ),则
=(sinθ,2,cos θ),则