题目内容
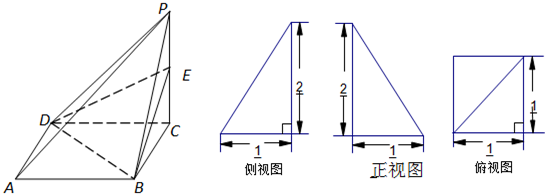
已知四棱锥P-ABCD的三视图如图所示，E是侧棱PC上的动点．
（1）求四棱锥P-ABCD的体积；
（2）求证：PA∥平面DBE．
（1）求四棱锥P-ABCD的体积；
（2）求证：PA∥平面DBE．
分析：（1）四棱锥的底面是一个边长是1的正方形，一条侧棱与底面垂直，由这条侧棱长是2知四棱锥的高是2，求四棱锥的体积只要知道底面大小和高，就可以得到结果．
（2）连接AC，交BD于O，连接OE，证明OE∥PA，由线面平行的判定定理可证PA∥平面BDE．
（2）连接AC，交BD于O，连接OE，证明OE∥PA，由线面平行的判定定理可证PA∥平面BDE．
解答：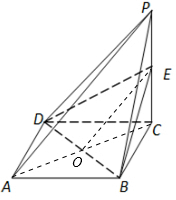
解：（1）、由三视图知，四棱锥的底面是一个边长是1的正方形，
一条侧棱与底面垂直，由这条侧棱长是2知四棱锥的高是2，
∴四棱锥的体积V=
×1×2=
，
（2）连接AC，交BD于O，连接OE，
∵四棱锥的底面是正方形，∴O为AC的中点，
∴OE∥PA，PA?平面BDE，OE?平面BDE，
∴PA∥平面BDE．
解：（1）、由三视图知，四棱锥的底面是一个边长是1的正方形，一条侧棱与底面垂直，由这条侧棱长是2知四棱锥的高是2，
∴四棱锥的体积V=
| 1 |
| 3 |
| 2 |
| 3 |
（2）连接AC，交BD于O，连接OE，
∵四棱锥的底面是正方形，∴O为AC的中点，
∴OE∥PA，PA?平面BDE，OE?平面BDE，
∴PA∥平面BDE．
点评：本题考查由三视图求几何体的体积，考查线面平行的判定，本题解题的关键是看清四棱锥中存在一条和底面垂直的侧棱，这是求体积的关键．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．