题目内容
若 ,且
,且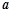 与
与 的夹角为
的夹角为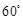 ,当
,当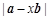 取得最小值时,实数
取得最小值时,实数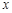 的值为( )
的值为( )
| A.2 | B. | C.1 | D. |
C
解析试题分析:利用平面向量模的平方等于向量的平方,得 =
= ,利用向量数量积运算法则及数量积的定义与性质得
,利用向量数量积运算法则及数量积的定义与性质得 =
= =
= ,知当
,知当 =1时,
=1时,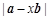 取最小值.
取最小值.
考点:1.平面向量的数量积的性质;2.平面向量数量积;3.二次函数的最值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
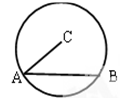
如图,半径为R的圆C中,已知弦AB的长为5,则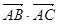 =( )
=( )
A.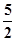 | B.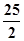 | C.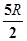 | D.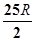 |
若 是夹角为60°的两个单位向量,则
是夹角为60°的两个单位向量,则 与
与 的夹角为( )
的夹角为( )
| A.30° | B.60° | C.120° | D.150° |
已知向量 ,
, 满足:
满足: ,且
,且 (
( ).则向量
).则向量 与向量
与向量 的夹角的最大值为( ).
的夹角的最大值为( ).
A. | B. | C. | D. |
设 为
为 所在平面上一点,动点
所在平面上一点,动点 满足
满足 ,其中
,其中 为
为 的三个内角,则点
的三个内角,则点 的轨迹一定通过
的轨迹一定通过 的()
的()
| A.外心 | B.内心 | C.重心 | D.垂心 |
在 中,
中, ( )
( )
A. | B. | C. | D. |
在 中, 已知向量
中, 已知向量 ,
,  ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
已知平面内两个定点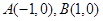 ,过动点
,过动点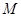 作直线
作直线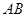 的垂线,垂足为
的垂线,垂足为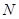 .若
.若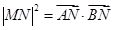 ,则动点
,则动点 的轨迹是( )
的轨迹是( )
| A.圆 | B.抛物线 | C.椭圆 | D.双曲线 |
 ,则
,则 的夹角为( )
的夹角为( )


