题目内容
过直线 上的一点作圆
上的一点作圆 的两条切线
的两条切线 ,当直线
,当直线 关于
关于 对称时,它们之间的夹角为( )
对称时,它们之间的夹角为( )
 上的一点作圆
上的一点作圆 的两条切线
的两条切线 ,当直线
,当直线 关于
关于 对称时,它们之间的夹角为( )
对称时,它们之间的夹角为( )| A.30° | B.45° | C.60° | D.90° |
C
过圆心M作直线l:y=x的垂线交于N点,过N点作圆的切线能够满足条件,不难求出夹角为600.
明白N点后,用图象法解之也很方便
解:圆(x-5)2+(y-1)2=2的圆心(5,1),过(5,1)与y=x垂直的直线方程:x+y-6=0,它与y="x" 的交点N(3,3),
N到(5,1)距离是2 ,两条切线l1,l2,它们之间的夹角为60°.
,两条切线l1,l2,它们之间的夹角为60°.
故选C.
明白N点后,用图象法解之也很方便
解:圆(x-5)2+(y-1)2=2的圆心(5,1),过(5,1)与y=x垂直的直线方程:x+y-6=0,它与y="x" 的交点N(3,3),
N到(5,1)距离是2
 ,两条切线l1,l2,它们之间的夹角为60°.
,两条切线l1,l2,它们之间的夹角为60°.故选C.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
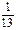
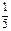
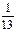
 是圆
是圆 内异于圆心的一点,则直线
内异于圆心的一点,则直线 与圆
与圆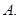 相交
相交  相切
相切  相离
相离  不能确定
不能确定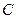 :
: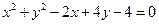 .问在圆
.问在圆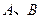 关于直线
关于直线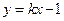 对称,且以
对称,且以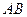 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线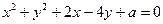 关于直线
关于直线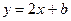 成轴对称,则
成轴对称,则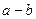 的取值范围是________.
的取值范围是________. 相切的圆的标准方程为 _________________.
相切的圆的标准方程为 _________________.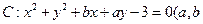 为正实数)上任意一点关于直线
为正实数)上任意一点关于直线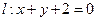 的对称点都在圆C上,则
的对称点都在圆C上,则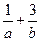 的最小值为 .
的最小值为 . ,圆
,圆 ,过圆
,过圆 上任一点
上任一点 作圆
作圆 的切线
的切线 ,若直线
,若直线 ,则当弦
,则当弦 的长度最大时,直线
的长度最大时,直线 、
、 且圆心在直线
且圆心在直线 上的圆的标准方程并判断点
上的圆的标准方程并判断点 与圆的关系.
与圆的关系.