题目内容
已知不等式x2-5mx+4m2≤0的解集为A,不等式ax2-x+1-a<0的解集为B.(1)求A;
(2)若m=1时,A∩B=A,求a的取值范围.
分析:(1)将一元二次不等式因式分解,两根的大小引起对m的讨论,求出集合A.
(2)求出集合A,将A∩B=A转化为A⊆B;通过对二次项的符号的讨论,求出集合B,判断出集合A,B的端点的大小,求出a的范围.
(2)求出集合A,将A∩B=A转化为A⊆B;通过对二次项的符号的讨论,求出集合B,判断出集合A,B的端点的大小,求出a的范围.
解答:解:(1)不等式x2-5mx+4m2≤0可化为:(x-m)(x-4m)≤0
①当m>0时,A=[m,4m]
②当m=0时,A={0}
③当m<0时,A=[4m,m]
(2)m=1时,A=[1,4]
不等式ax2-x+1-a<0可化为[ax-(1-a)](x-1)<0
∵A∩B=A,
∴A⊆B
当a>0时,
>4
∴0<a<
当a=0时,B={x|x>1}合题意
当a<0时,B={x|x>1或x<
}合题意
总之,a<
①当m>0时,A=[m,4m]
②当m=0时,A={0}
③当m<0时,A=[4m,m]
(2)m=1时,A=[1,4]
不等式ax2-x+1-a<0可化为[ax-(1-a)](x-1)<0
∵A∩B=A,
∴A⊆B
当a>0时,
| 1-a |
| a |
∴0<a<
| 1 |
| 5 |
当a=0时,B={x|x>1}合题意
当a<0时,B={x|x>1或x<
| 1-a |
| a |
总之,a<
| 1 |
| 5 |
点评:解二次不等式时,若含参数,一般要讨论,讨论的起点往往是二次项系数的符号、判别式的符号、两个根的大小.

练习册系列答案
 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
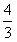 )x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。
)x+6在(-∞,+∞)上有极值;求使P正确且Q正确的m的取值范围。 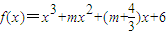 在(-∞,+∞)上有极值.求使P正确且Q正确的m的取值范围.
在(-∞,+∞)上有极值.求使P正确且Q正确的m的取值范围.