题目内容
已知等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,等比数列
,等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,存在
,存在![]() 使得
使得![]() 成立,其中
成立,其中![]() 均为正整数,且
均为正整数,且![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)设函数![]() 是函数
是函数![]() 的导函数;令
的导函数;令![]() ,求
,求![]() (用含
(用含![]() 的代数式表示)。
的代数式表示)。
解: ![]()
![]() ………………………………………2分
………………………………………2分
又![]()
若![]() 则
则![]() 矛盾…………………………………3分
矛盾…………………………………3分
![]() ……………………………………………………………………………………4分
……………………………………………………………………………………4分
又因为![]()
![]()
![]() …………
…………![]() ………………………………………………………7分
………………………………………………………7分
(2)![]() …………………………………8分
…………………………………8分
![]() ……………………………………………9分
……………………………………………9分
得![]() ………………………10分[来源:学.科.网Z.X.X.K]
………………………10分[来源:学.科.网Z.X.X.K]
记![]() (1)
(1)
![]() (2)[来源:学科网]
(2)[来源:学科网]
(2)-(1)得![]() …………………………13分
…………………………13分
![]() 即
即![]() .………………………………14分
.………………………………14分

练习册系列答案
相关题目
 的首项为
的首项为 ,公差为
,公差为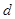 ,其前
,其前 项和为
项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则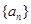 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列 的首项为b,公比为a,其中a,b均为正整数,若
的首项为b,公比为a,其中a,b均为正整数,若 。
。 成等比数列,求数列
成等比数列,求数列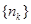 的通项公式。
的通项公式。
 的前n项和为
的前n项和为 ,求当
,求当 最大时,n的值。
最大时,n的值。 的首项为24,公差为
的首项为24,公差为 ,则当n=
时,该数列的前n项
,则当n=
时,该数列的前n项 取得最大值.
取得最大值.