题目内容
已知点H（-6，0），点P（0，b）在y轴上，点Q（a，0）在x轴的正半轴上，且满足
⊥
，点M在直线PQ上，且满足
=2
．
（Ⅰ）当点P在y轴上移动时，求点M的轨迹方程；
（Ⅱ）若点M在曲线C：
（t为参数）上，求点M对应的参数t（0＜t＜2π）的值．
| HP |
| PQ |
| PM |
| MQ |
（Ⅰ）当点P在y轴上移动时，求点M的轨迹方程；
（Ⅱ）若点M在曲线C：
|
考点：参数方程化成普通方程
专题：坐标系和参数方程
分析：对第（Ⅰ）问，先设点M坐标为（x，y），写出向量
，
，
，
的坐标，由
⊥
及
=2
得到三个方程，消去a，b，可得x与y的关系式；
对第（Ⅱ）问，由题意知，点M为第（Ⅰ）问中所求轨迹与曲线C的交点，可联立此两曲线的方程，消去x与y，即得参数t的值．
| HP |
| PQ |
| PM |
| MQ |
| HP |
| PQ |
| PM |
| MQ |
对第（Ⅱ）问，由题意知，点M为第（Ⅰ）问中所求轨迹与曲线C的交点，可联立此两曲线的方程，消去x与y，即得参数t的值．
解答：
解析：（Ⅰ）设点M的坐标为（x，y），
则
=(6，b)，
=(a，-b)，
=(x，y-b)，
=(a-x，-y)，
由
⊥
，得（6，b）•（a，-b）=0，从而6a-b2=0，即a=
．…①
由
=2
，得（x，y-b）=2（a-x，-y），从而
，即
，…②
将①式代入②式中，得
，消去b，得y2=x，
又由点Q（a，0）在x轴的正半轴上知，a＞0，从而x＞0，
故点M的轨迹C的方程为y2=x（x＞0）．
（Ⅱ）依题意，将
代入y2=x（x＞0）中，
得2sin2t=3cost，即2cos2t+3cost-2=0，
解得cost=
，
又0＜t＜2π，∴t=
，
，
即点M对应的参数t（0＜t＜2π）的值为
，
．
则
| HP |
| PQ |
| PM |
| MQ |
由
| HP |
| PQ |
| b2 |
| 6 |
由
| PM |
| MQ |
|
|
将①式代入②式中，得
|
又由点Q（a，0）在x轴的正半轴上知，a＞0，从而x＞0，
故点M的轨迹C的方程为y2=x（x＞0）．
（Ⅱ）依题意，将
|
得2sin2t=3cost，即2cos2t+3cost-2=0，
解得cost=
| 1 |
| 2 |
又0＜t＜2π，∴t=
| π |
| 3 |
| 5π |
| 3 |
即点M对应的参数t（0＜t＜2π）的值为
| π |
| 3 |
| 5π |
| 3 |
点评：1．求轨迹方程的一般步骤是：
（1）建系：建系的一般原则是，尽量使题设中的点、线在坐标轴上，本题中坐标系已经建好；
（2）设点：已知图形中的点常设为（x0，y0），（x1，y1），（x2，y2）等，轨迹上任意一点可设M（x，y）；
（3）列式：即寻找x与y的等量关系，本题通过消参的方式得到了x与y的等量关系，这是最关键的一步；
（4）化简并检验：舍去多余的值，增加遗漏的值，如本题中“x=0”是不合题意的，应舍去．
2．第（Ⅱ）问考查了参数方程的应用，对于两曲线的交点问题，若是求交点坐标，一般是消参后，解两普通方程构成的方程组，或求参数的值，将参数的值代入参数方程中，均可得交点坐标；若是求参数方程中参数的值，一般是将参数方程代入普通方程中，消去x与y，即可得参数的值．
（1）建系：建系的一般原则是，尽量使题设中的点、线在坐标轴上，本题中坐标系已经建好；
（2）设点：已知图形中的点常设为（x0，y0），（x1，y1），（x2，y2）等，轨迹上任意一点可设M（x，y）；
（3）列式：即寻找x与y的等量关系，本题通过消参的方式得到了x与y的等量关系，这是最关键的一步；
（4）化简并检验：舍去多余的值，增加遗漏的值，如本题中“x=0”是不合题意的，应舍去．
2．第（Ⅱ）问考查了参数方程的应用，对于两曲线的交点问题，若是求交点坐标，一般是消参后，解两普通方程构成的方程组，或求参数的值，将参数的值代入参数方程中，均可得交点坐标；若是求参数方程中参数的值，一般是将参数方程代入普通方程中，消去x与y，即可得参数的值．
练习册系列答案
相关题目
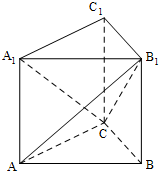直三棱柱ABC-A1B1C1中，AC=BC=BB1=1，AB=
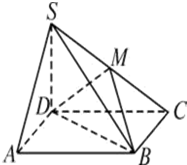如图四棱锥S-ABCD，底面ABCD是正方形，SD⊥底面ABCD，M为SC的中点．
如图是甲、乙两名同学在五场篮球比赛中得分情况的茎叶图，那么甲、乙两人和分的标准差s甲