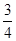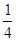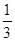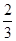题目内容
在直角坐标系xOy中,已知中心在原点,离心率为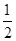 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设P是椭圆E上一点,过P作两条斜率之积为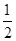 的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
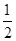 的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.
的椭圆E的一个焦点为圆C:x2+y2-4x+2=0的圆心.(Ⅰ)求椭圆E的方程;
(Ⅱ)设P是椭圆E上一点,过P作两条斜率之积为
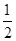 的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.
的直线l1,l2.当直线l1,l2都与圆C相切时,求P的坐标.(Ⅰ)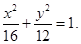 (Ⅱ)
(Ⅱ)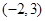 ,或
,或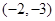 ,或
,或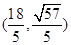 ,或
,或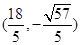 .
.
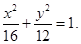 (Ⅱ)
(Ⅱ)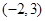 ,或
,或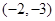 ,或
,或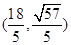 ,或
,或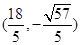 .
.(Ⅰ)由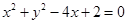 ,得
,得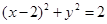 .故圆C的圆心为点
.故圆C的圆心为点
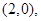 从而可设椭圆E的方程为
从而可设椭圆E的方程为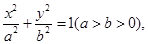 其焦距为
其焦距为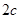 ,由题设知
,由题设知
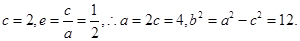 故椭圆E的方程为:
故椭圆E的方程为: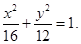
(Ⅱ)设点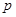 的坐标为
的坐标为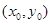 ,
,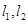 的斜分率分别为
的斜分率分别为 则
则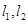 的方程分别为
的方程分别为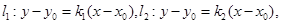 且
且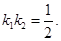 由
由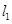 与圆
与圆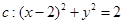 相切,得
相切,得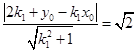 ,即
,即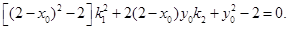
同理可得 .
.
从而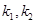 是方程
是方程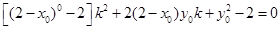 的两个实根,于是
的两个实根,于是
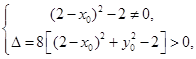 ①
①
且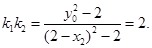
由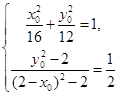 得
得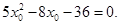 解得
解得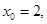 或
或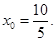
由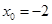 得
得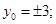 由
由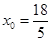 得
得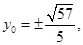 它们满足①式,故点P的坐标为
它们满足①式,故点P的坐标为
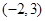 ,或
,或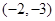 ,或
,或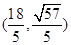 ,或
,或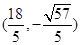 .
.
【点评】本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第一问根据条件设出椭圆方程,求出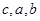 即得椭圆E的方程,第二问设出点P坐标,利用过P点的两条直线斜率之积为
即得椭圆E的方程,第二问设出点P坐标,利用过P点的两条直线斜率之积为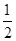 ,得出关于点P坐标的一个方程,利用点P在椭圆上得出另一方程,联立两个方程得点P坐标.
,得出关于点P坐标的一个方程,利用点P在椭圆上得出另一方程,联立两个方程得点P坐标.
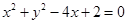 ,得
,得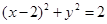 .故圆C的圆心为点
.故圆C的圆心为点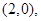 从而可设椭圆E的方程为
从而可设椭圆E的方程为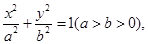 其焦距为
其焦距为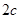 ,由题设知
,由题设知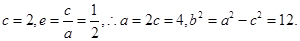 故椭圆E的方程为:
故椭圆E的方程为: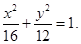
(Ⅱ)设点
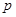 的坐标为
的坐标为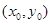 ,
,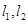 的斜分率分别为
的斜分率分别为 则
则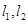 的方程分别为
的方程分别为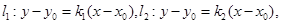 且
且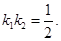 由
由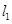 与圆
与圆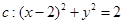 相切,得
相切,得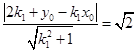 ,即
,即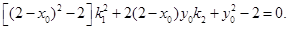
同理可得
 .
.从而
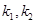 是方程
是方程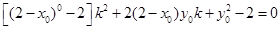 的两个实根,于是
的两个实根,于是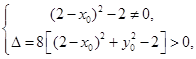 ①
①且
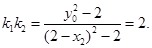
由
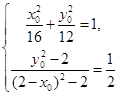 得
得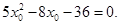 解得
解得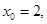 或
或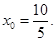
由
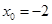 得
得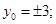 由
由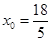 得
得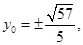 它们满足①式,故点P的坐标为
它们满足①式,故点P的坐标为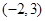 ,或
,或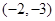 ,或
,或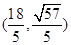 ,或
,或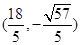 .
.【点评】本题考查曲线与方程、直线与曲线的位置关系,考查运算能力,考查数形结合思想、函数与方程思想等数学思想方法.第一问根据条件设出椭圆方程,求出
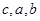 即得椭圆E的方程,第二问设出点P坐标,利用过P点的两条直线斜率之积为
即得椭圆E的方程,第二问设出点P坐标,利用过P点的两条直线斜率之积为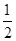 ,得出关于点P坐标的一个方程,利用点P在椭圆上得出另一方程,联立两个方程得点P坐标.
,得出关于点P坐标的一个方程,利用点P在椭圆上得出另一方程,联立两个方程得点P坐标.
练习册系列答案
相关题目
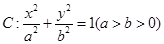 的焦点和上顶点分别为
的焦点和上顶点分别为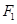 、
、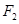 、
、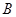 ,我们称
,我们称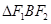 为椭圆
为椭圆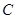 的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比.
的特征三角形.如果两个椭圆的特征三角形是相似的,则称这两个椭圆是“相似椭圆”,且三角形的相似比即为椭圆的相似比. 和
和 ,判断
,判断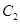 与
与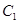 是否相似,如果相似则求出
是否相似,如果相似则求出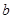 的椭圆为
的椭圆为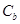 ,且直线
,且直线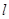 与椭圆为
与椭圆为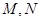 (异于端点),试问:当
(异于端点),试问:当 面积最大时,
面积最大时,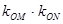 是否与
是否与
 上的一点,点M、N分别是两圆:
上的一点,点M、N分别是两圆: 和
和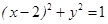 上的点,则的最小值、最大值分别为( )
上的点,则的最小值、最大值分别为( )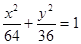 上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______.
上一点P到它的一个焦点的距离等于4,那么点P到另一个焦点的距离等于_______.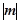
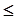 2,椭圆
2,椭圆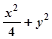 =1,p在椭圆上移动,求
=1,p在椭圆上移动,求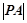 的最小值.
的最小值.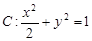 的左、右焦点分别为
的左、右焦点分别为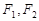 ,下顶点为
,下顶点为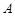 ,点
,点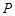 是椭圆上任一点,圆
是椭圆上任一点,圆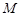 是以
是以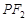 为直径的圆.
为直径的圆.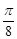 ,求
,求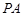 所在的直线方程;
所在的直线方程;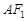 相切时,求圆
相切时,求圆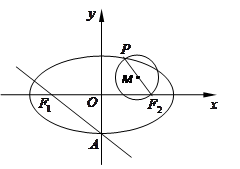
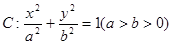 的离心率为
的离心率为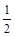 ,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+
,以原点为圆心,椭圆的短半轴为半径的圆与直线x-y+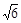 =0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.
=0相切,过点P(4,0)的直线L与椭圆C相交于A、B两点.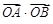 的取值范围.
的取值范围.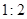 ,则此椭圆离心率的取值范围是( )
,则此椭圆离心率的取值范围是( )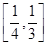
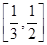
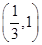
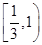
 有公共的焦点F1,F2,P是两曲线的一个交点,则
有公共的焦点F1,F2,P是两曲线的一个交点,则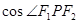 =( )
=( )