题目内容
【题目】设
，函数
的最小值为
.
（1）求的解析式
（2）画出函数
的大致图形
（3）求函数的最值
【答案】（1）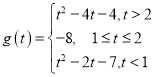
；（2）作图见详解；
（3）
最小值为
，无最大值
【解析】
（1）由于函数
对称轴为
，分对称轴在闭区间的左边、中间、右边三种情况，分别求得函数
的最小值，可得
的解析式.
（2）根据（1）中的解析式，作出分段函数的图像即可.
由（2）的图像，观察即可求得函数的最值.
（1）由于函数对称轴为，
当
时，函数
在闭区间
上单调递增，
故函数的最小值为
；
当
，即
时，故函数的最小值
；
当
，即
时，函数在闭区间上单调递减，
故函数的最小值为
；
综上所述，，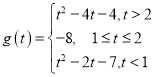
（2）作出的图像，如图所示：
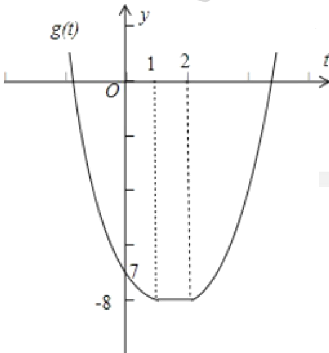
（3）由（2）的图像，函数的最小值为，无最大值.
综上所述，函数的最小值为，无最大值.
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
