题目内容
已知函数f(x)=mx3+nx,y=f(x)的图象在以点 为切点的切线的倾斜角为
为切点的切线的倾斜角为 .
.
(1)求m、n的值;
(2)求函数y=f(x)在[-2,1]上的最大值和最小值.
解:(1)求导函数,可得f′(x)=3mx2+n
由题意有 ,解得
,解得
(2)由(1)知 ,所以f′(x)=2x2-1
,所以f′(x)=2x2-1
令f′(x)=2x2-1=0,可得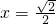
列表
由上表可知f(x)的最大值为 ,最小值为
,最小值为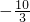 .
.
分析:(1)求导函数,利用y=f(x)的图象在以点 为切点的切线的倾斜角为
为切点的切线的倾斜角为 ,建立方程,即可求得求m、n的值;
,建立方程,即可求得求m、n的值;
(2)求导函数,确定极值点,求出端点函数值与函数的极值,即可求得函数y=f(x)在[-2,1]上的最大值和最小值.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,正确求导是关键.
由题意有
 ,解得
,解得
(2)由(1)知
 ,所以f′(x)=2x2-1
,所以f′(x)=2x2-1令f′(x)=2x2-1=0,可得
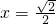
列表
| x | -2 |  |  |  |  |  | 1 |
| f′(x) | + | - | + | ||||
| f(x) | 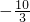 | 递增 | 极大值 | 递减 | 极小值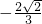 | 递增 |  |
 ,最小值为
,最小值为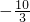 .
.分析:(1)求导函数,利用y=f(x)的图象在以点
 为切点的切线的倾斜角为
为切点的切线的倾斜角为 ,建立方程,即可求得求m、n的值;
,建立方程,即可求得求m、n的值;(2)求导函数,确定极值点,求出端点函数值与函数的极值,即可求得函数y=f(x)在[-2,1]上的最大值和最小值.
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性与最值,正确求导是关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目