题目内容
【题目】已知椭圆![]() 的长轴长为
的长轴长为![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程和离心率.
的方程和离心率.
(2)设点![]() ,动点
,动点![]() 在
在![]() 轴上,动点
轴上,动点![]() 在椭圆
在椭圆![]() 上,且点
上,且点![]() 在
在![]() 轴的右侧.若
轴的右侧.若![]() ,求四边形
,求四边形![]() 面积的最小值.
面积的最小值.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() .
.
【解析】(1)由已知,将椭圆方程转化为标准形式,确定其长轴、短轴,并求出参数![]() 的值,从而求出椭圆方程及其离心率;(2)根据题意结合草图,易知
的值,从而求出椭圆方程及其离心率;(2)根据题意结合草图,易知![]() ,通过动点
,通过动点![]() 的坐标求出点
的坐标求出点![]() 的坐标,将四边形
的坐标,将四边形![]() 分割成三角形
分割成三角形![]() 和三角形
和三角形![]() 进行运算即可.
进行运算即可.
试题解析:(1)由题意知椭圆![]()
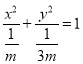 ,
,
所以![]() ,
, ![]() ,
,
故![]() ,
,
解得![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
因为![]() ,
,
所以离心率![]() .
.
(2)设线段![]() 的中点为
的中点为![]() .
.
因为![]() ,所以
,所以![]() .
.
由题意知直线![]() 的斜率存在,
的斜率存在,
设点![]() 的坐标为
的坐标为![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
所以直线![]() 的斜率
的斜率![]() ,
,
故直线![]() 的方程为
的方程为![]() .
.
令![]() ,得
,得![]() ,故
,故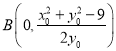 .
.
由![]() ,得
,得![]() ,化简得
,化简得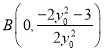 .
.
因此, ![]()
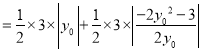
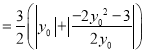
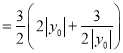
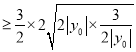
![]() .
.
当且仅当![]() 时,即
时,即![]() 时等号成立.
时等号成立.
故四边形![]() 面积的最小值为
面积的最小值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目