题目内容
6.若方程a|x|=log2(x+2)+1有且只有一个实根,则实数a的取值范围是(0,1].分析 先将方程两边看成两个函数,再通过分类讨论并结合函数图象确定参数a的取值范围.
解答 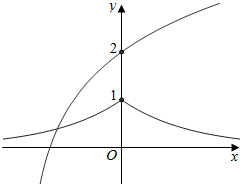 解:设y1=a|x|,y2=log2(x+2)+1,
解:设y1=a|x|,y2=log2(x+2)+1,
对a分类讨论如下:
①当a=1时,y1=1为常数函数,
与函数y2的图象只有一个交点,符合题意;
②当a>1时,y1为偶函数,图象关于y轴对称,
且x<0时,函数y1递减,x>0时,函数y1递增,
因此,函数y1与y2的图象有两个交点;
③当0<a<1时,y1为偶函数,如右图,
且x<0时,函数y1递增,x>0时,函数y1递减,
因此,函数y1与y2的图象只有一个交点;
综合以上讨论得,a∈(0,1].
故答案为:(0,1].
点评 本题主要考查了指数函数的图象和性质,以及根的存在和个数的判断,体现了分类讨论和数形结合的解题思想,属于中档题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
1.定义在R上的偶函数f(x),对任意实数x都有f(x+2)=f(x),当x∈[0,1]时,f(x)=x2,若在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是( )
| A. | $(-\frac{1}{4},\frac{1}{4}]$ | B. | $(0,\frac{1}{4}]$ | C. | $(\frac{1}{4},\frac{1}{3}]$ | D. | $(0,\frac{1}{3})$ |
11.已知集合$A=\{x|y=\sqrt{4-{x^2}}\}$,B={y|y=x2-x+1,0<x<2},则A∩B=( )
| A. | $(\frac{3}{4},2]$ | B. | [2,3) | C. | (1,2] | D. | (-∞,-2]∪[2,+∞) |
12.设 f(x)=$\left\{\begin{array}{l}x-2\\ f(x+6)\end{array}$$\begin{array}{l}({x≥10})\\({x<10})\end{array}$,则f(5)的值为( )
| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
13.在等比数列{an}中,下列各式中成立的是( )
| A. | a8=a2a4 | B. | a6=a2+a4 | C. | ${a_4}^2={a_2}{a_6}$ | D. | ${a_8}^2={a_2}{a_6}$ |
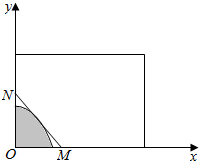 如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M、N,则当能开发的面积达到最大时,OM的长为1.
如图,某房地产公司要在一块矩形宽阔地面上开发物业,阴影部分是不能开发的古建筑群,且要求用在一条直线上的栏栅进行隔离,古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分,栏栅与矩形区域边界交于点M、N,则当能开发的面积达到最大时,OM的长为1. 是定义在
是定义在 上的偶函数,
上的偶函数, ,有
,有 ,则( )
,则( )



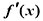 ,当x<0时,f(x)满足
,当x<0时,f(x)满足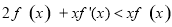 ,则f(x)在R上的零点个数为( )
,则f(x)在R上的零点个数为( )