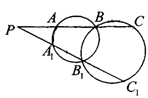
题目内容
如图,圆 的圆心
的圆心 在
在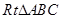 的直角边
的直角边 上,该圆与直角边
上,该圆与直角边 相切,与斜边
相切,与斜边 交于
交于 ,
, ,
, .
.

(1)求 的长;
的长;
(2)求圆 的半径.
的半径.
 的圆心
的圆心 在
在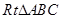 的直角边
的直角边 上,该圆与直角边
上,该圆与直角边 相切,与斜边
相切,与斜边 交于
交于 ,
, ,
, .
.
(1)求
 的长;
的长; (2)求圆
 的半径.
的半径.(1) ;(2)
;(2) .
.
 ;(2)
;(2) .
.试题分析:(1)根据已知条件及切割线定理,得
 ,然后在
,然后在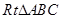 应用勾股定理可计算出
应用勾股定理可计算出 的长度;(2)设圆
的长度;(2)设圆 的半径为
的半径为 ,由切割线定理,并结合(1)中的计算,可得
,由切割线定理,并结合(1)中的计算,可得 ,即
,即 ,从中求解即可得到
,从中求解即可得到 的值.
的值.试题解析:(1)由已知及切割线定理,有

所以
 3分
3分因为
 ,所以
,所以
在
 中,由勾股定理得,
中,由勾股定理得, 5分
5分
(2)设圆
 与
与 的交点为
的交点为 ,圆
,圆 的半径为
的半径为
由割线定理,得
 8分
8分即
 ,从中解得
,从中解得 10分.
10分.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
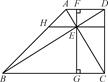


 (2)若AD=2,CD=3.DB=4,求
(2)若AD=2,CD=3.DB=4,求 的值.
的值.
 AC,AE=
AC,AE= AB,BD,CE相交于点F.
AB,BD,CE相交于点F.

 切圆
切圆 于点
于点 ,割线
,割线 经过圆心
经过圆心 ,
, 绕点
绕点 到
到 ,则
,则 的长为 .
的长为 .
 =
= ,
, =
= ,则
,则 的值为______.
的值为______.
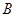 、
、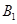 ,直线
,直线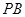 与
与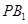 分别与两圆交于点
分别与两圆交于点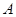 、
、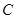 和
和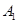 、
、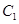 ,
,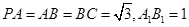 ,则
,则 .
.