题目内容
将数列![]() 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表:

记表中的第一列数a1,a2,,a4,a7,…构成的数列为![]() ,b1=a1=1.Sn为数列的
,b1=a1=1.Sn为数列的![]()
前n项和, 且满足![]() .
.
(I)证明数列![]() 成等差数列, 并求数列
成等差数列, 并求数列![]() 的通项公式;
的通项公式;
(II)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同个正数,当![]() 时,求上表中第
时,求上表中第![]() 行所有项的和。
行所有项的和。
证明:由已知,当![]() 时,
时,![]() 又
又![]()
所以![]() ,所以
,所以![]() ,又
,又![]() 所以数列
所以数列![]() 是首项为1,公差为
是首项为1,公差为![]() 的等差数列。由上可知
的等差数列。由上可知![]() 即
即![]() .所以当
.所以当![]() 时,
时,![]() 因此
因此 .
.
(Ⅱ)解:设上表中从第三行起,每行的公比都为![]() ,且
,且![]() >0,因为
>0,因为![]() ,所以表中第1行至第12行共含有数列
,所以表中第1行至第12行共含有数列![]() 的前78项,故
的前78项,故![]() 在表中第13行第三列,因此
在表中第13行第三列,因此![]() 。又
。又![]() ,所以
,所以![]() 。记表中第
。记表中第![]() 。
。

练习册系列答案
相关题目
(本小题满分14分)
已知函数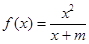 的图像经过点
的图像经过点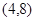 .
.
(1)求该函数的解析式;
(2)数列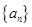 中,若
中,若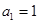 ,
,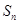 为数列
为数列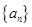 的前
的前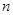 项和,且满足
项和,且满足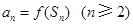 ,
,
证明数列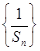 成等差数列,并求数列
成等差数列,并求数列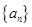 的通项公式;
的通项公式;
(3)另有一新数列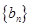 ,若将数列
,若将数列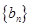 中的所有项按每一行比上一行多一项的规则排成
中的所有项按每一行比上一行多一项的规则排成
如下数表:
|
|
|
|
|
|
|
|
记表中的第一列数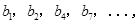 构成的数列即为数列
构成的数列即为数列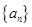 ,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
,上表中,若从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当
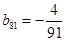 时,求上表中第
时,求上表中第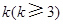 行所有项的和.
行所有项的和.
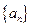 中的所有项按每一行比上一行多一项的规则排成如下数表
中的所有项按每一行比上一行多一项的规则排成如下数表 :
: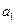
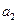
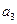
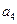
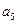
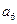
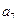
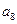
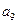
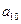
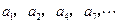 构成的数列为
构成的数列为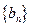 ,
,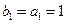 .
.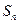 为数列
为数列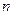 项和,且满足
项和,且满足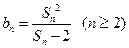 .
.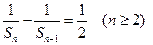 ;
;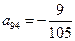 时,求上表中第
时,求上表中第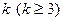 行所有项的和.
行所有项的和.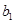
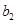
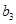
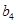
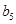
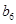
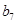
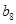
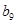
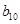
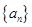 中的所有项按每一行比上一行多一项的规则排成如下数表:
中的所有项按每一行比上一行多一项的规则排成如下数表: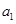
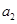
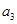
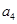
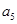
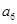
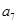
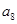
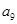
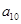
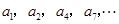 构成的数列为
构成的数列为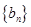 ,
,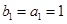 .
.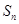 为数列
为数列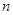 项和,且满足
项和,且满足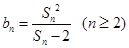 .
.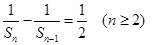 ;
;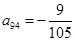 时,求上表中第
时,求上表中第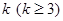 行所有项的和.
行所有项的和. 中的所有项按每一行比上一行多一项的规则排成下表:
中的所有项按每一行比上一行多一项的规则排成下表:









 ,
, ,
, 为数列
为数列 项和,且满足
项和,且满足
 成等差数列,并求数列
成等差数列,并求数列 时,求上表中第
时,求上表中第 行所有项的和
行所有项的和