题目内容
若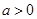 且
且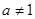 ,且
,且 ,则实数
,则实数 的取值范围( )
的取值范围( )
A.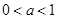 | B. |
C. 或 或 | D.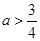 或 或 |
C
解析试题分析:根据题意,由于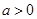 且
且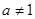 ,且
,且 成立,
成立,
当0<a<1时,根据对数函数递减性质可知, ,故可知范围是
,故可知范围是 ,综上可知
,综上可知
实数 的取值范围C
的取值范围C
考点:不等式
点评:主要是考查了对数不等式的求解,属于基础题。

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
为了得到函数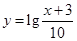 的图像,只需把函数
的图像,只需把函数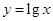 的图像上所有的点( )
的图像上所有的点( )
| A.向左平移3个单位长度,再向上平移1个单位长度 |
| B.向右平移3个单位长度,再向上平移1个单位长度 |
| C.向左平移3个单位长度,再向下平移1个单位长度 |
| D.向右平移3个单位长度,再向下平移1个单位长度 |
定义运算 ,函数
,函数 图像的顶点是
图像的顶点是 ,且
,且 成等差数列,则
成等差数列,则 ( )
( )
| A.0 | B.-14 | C.-9 | D.-3 |
若 ,则( )
,则( )
A. | B. |
C. | D. |
下列大小关系正确的是
A. | B. |
C. | D. |
若定义在R上的函数f(x)满足 ,且
,且 <0a="f" (
<0a="f" ( ),b="f" (
),b="f" ( ),c="f" (
),c="f" ( ),则a,b,c的大小关系为
),则a,b,c的大小关系为
| A.a>b>c | B.c>b>a | C.b>a>c | D.c>a>b |
如果 ,那么
,那么 的最小值是( )
的最小值是( )
| A.4 | B. | C.9 | D.18 |
给定函数① ,②
,② ,③
,③ ,④
,④ ,
,
其中在区间(0,1)上单调递减的函数序号是( )
| A.①② | B.②③ | C.③④ | D.①④ |
 ,形状为直角三角形的铁架框,有下列四种长度的铁管供选择,较经济(够用,又耗材最少)的是
,形状为直角三角形的铁架框,有下列四种长度的铁管供选择,较经济(够用,又耗材最少)的是 


