题目内容
已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与
与![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线 C.
的轨迹为曲线 C.
(Ⅰ)求C的方程;
(Ⅱ)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
【解析】由已知得圆![]() 的圆心为
的圆心为![]() (-1,0),半径
(-1,0),半径![]() =1,圆
=1,圆![]() 的圆心为
的圆心为![]() (1,0),半径
(1,0),半径![]() =3.
=3.
设动圆![]() 的圆心为
的圆心为![]() (
(![]() ,
,![]() ),半径为R.
),半径为R.
(Ⅰ)∵圆![]() 与圆
与圆![]() 外切且与圆
外切且与圆![]() 内切,∴|PM|+|PN|=
内切,∴|PM|+|PN|=![]() =
=![]() =4,
=4,
由椭圆的定义可知,曲线C是以M,N为左右焦点,场半轴长为2,短半轴长为![]() 的椭圆(左顶点除外),其方程为
的椭圆(左顶点除外),其方程为![]() .
.
(Ⅱ)对于曲线C上任意一点![]() (
(![]() ,
,![]() ),由于|PM|-|PN|=
),由于|PM|-|PN|=![]() ≤2,∴R≤2,
≤2,∴R≤2,
当且仅当圆P的圆心为(2,0)时,R=2.
∴当圆P的半径最长时,其方程为![]() ,
,
当![]() 的倾斜角为
的倾斜角为![]() 时,则
时,则![]() 与
与![]() 轴重合,可得|AB|=
轴重合,可得|AB|=![]() .
.
当![]() 的倾斜角不为
的倾斜角不为![]() 时,由
时,由![]() ≠R知
≠R知![]() 不平行
不平行![]() 轴,设
轴,设![]() 与
与![]() 轴的交点为Q,则
轴的交点为Q,则![]() =
=![]() ,可求得Q(-4,0),∴设
,可求得Q(-4,0),∴设![]() :
:![]() ,由
,由![]() 于圆M相切得
于圆M相切得![]() ,解得
,解得![]() .
.
当![]() =
=![]() 时,将
时,将![]() 代入
代入![]() 并整理得
并整理得![]() ,解得
,解得![]() =
=![]() ,∴|AB|=
,∴|AB|=![]() =
=![]() .
.
当![]() =-
=-![]() 时,由图形的对称性可知|AB|=
时,由图形的对称性可知|AB|=![]() ,
,
综上,|AB|=![]() 或|AB|=
或|AB|=![]() .
.

练习册系列答案
相关题目
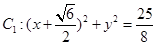 ,圆
,圆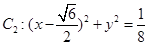 ,动圆
,动圆 与已知两圆都外切.
与已知两圆都外切. 的方程;
的方程;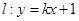 与点
与点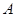 、
、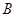 ,
,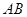 的中垂线与
的中垂线与 轴交于点
轴交于点 ,求点
,求点 ,圆
,圆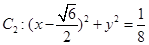 ,动圆
,动圆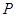 与已知两圆都外切.
与已知两圆都外切.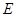 的方程(2)直线
的方程(2)直线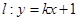 与点
与点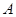 、
、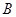 ,
,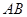 的中垂线与
的中垂线与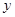 轴交于点
轴交于点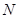 ,求点
,求点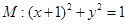 ,圆
,圆 ,动圆
,动圆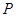 与圆
与圆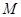 外切并且与圆
外切并且与圆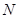 内切,圆心
内切,圆心 。
。 是与圆
是与圆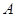 ,
,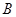 两点,当圆
两点,当圆 。
。 和圆
和圆 ,动圆M同时与圆C1及圆C2外切,则动圆圆心M的轨迹方程为 .
,动圆M同时与圆C1及圆C2外切,则动圆圆心M的轨迹方程为 . ,圆
,圆 .
. ,求直线l的方程;
,求直线l的方程;