题目内容
等差数列{an} 中,a1=1,前n项和Sn满足条件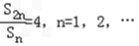 ,
,
(Ⅰ)求数列{an} 的通项公式和Sn;
(Ⅱ)记bn=an 2n﹣1,求数列{bn}的前n项和Tn.
2n﹣1,求数列{bn}的前n项和Tn.
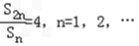 ,
,(Ⅰ)求数列{an} 的通项公式和Sn;
(Ⅱ)记bn=an
 2n﹣1,求数列{bn}的前n项和Tn.
2n﹣1,求数列{bn}的前n项和Tn. 解:(Ⅰ)设等差数列的公差为d,
由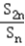 =4得
=4得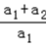 =4,
=4,
所以a2=3a1=3且d=a2﹣a1=2,
所以an=a1+(n﹣1)d=2n﹣1,
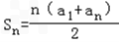 =
= 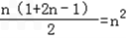
(Ⅱ)由bn=an 2n﹣1,得bn=(2n﹣1)
2n﹣1,得bn=(2n﹣1) 2n﹣1.
2n﹣1.
所以Tn=1+3 21+5
21+5 22+…+(2n﹣1)
22+…+(2n﹣1) 2n﹣1 ①
2n﹣1 ①
2Tn=2+3 22+5
22+5 23+…+(2n﹣3)
23+…+(2n﹣3) 2n﹣1+(2n﹣1)
2n﹣1+(2n﹣1) 2n ②
2n ②
①﹣②得:﹣Tn=1+2 2+2
2+2 22+…+2
22+…+2 2n﹣1﹣(2n﹣1)
2n﹣1﹣(2n﹣1) 2n
2n
=2(1+2+22+…+2n﹣1)﹣(2n﹣1) 2 n﹣1
2 n﹣1
=2×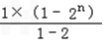 ﹣(2n﹣1)
﹣(2n﹣1) 2n﹣1
2n﹣1
=2n (3﹣2n)﹣3.
(3﹣2n)﹣3.
∴Tn=(2n﹣3) 2n+3.
2n+3.
由
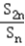 =4得
=4得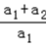 =4,
=4,所以a2=3a1=3且d=a2﹣a1=2,
所以an=a1+(n﹣1)d=2n﹣1,
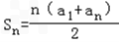 =
= 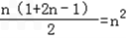
(Ⅱ)由bn=an
 2n﹣1,得bn=(2n﹣1)
2n﹣1,得bn=(2n﹣1) 2n﹣1.
2n﹣1.所以Tn=1+3
 21+5
21+5 22+…+(2n﹣1)
22+…+(2n﹣1) 2n﹣1 ①
2n﹣1 ① 2Tn=2+3
 22+5
22+5 23+…+(2n﹣3)
23+…+(2n﹣3) 2n﹣1+(2n﹣1)
2n﹣1+(2n﹣1) 2n ②
2n ② ①﹣②得:﹣Tn=1+2
 2+2
2+2 22+…+2
22+…+2 2n﹣1﹣(2n﹣1)
2n﹣1﹣(2n﹣1) 2n
2n=2(1+2+22+…+2n﹣1)﹣(2n﹣1)
 2 n﹣1
2 n﹣1 =2×
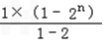 ﹣(2n﹣1)
﹣(2n﹣1) 2n﹣1
2n﹣1 =2n
 (3﹣2n)﹣3.
(3﹣2n)﹣3.∴Tn=(2n﹣3)
 2n+3.
2n+3. 
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目