题目内容
等差数列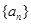 的前n项和为
的前n项和为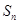 ,已知
,已知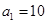 ,
,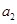 为整数,且
为整数,且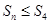 .
.
(1)求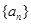 的通项公式;
的通项公式;
(2)设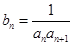 ,求数列
,求数列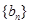 的前n项和
的前n项和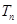 .
.
(1) ;(2)
;(2) .
.
解析试题分析:(1)由已知可得等差数列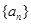 的公差
的公差 为整数.由
为整数.由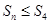 可得
可得 列出不等式组解得
列出不等式组解得 的范围,从而可确定整数
的范围,从而可确定整数 的值,最后由等差数列的通项公式可求得数列
的值,最后由等差数列的通项公式可求得数列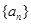 的通项公式;
的通项公式;
(2)由已知先写出 ,
,
列出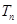 的表达式
的表达式 ,
,
由于 可分裂为
可分裂为 ,故采用裂项相消法求
,故采用裂项相消法求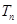 .
.
(1)由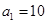 ,
,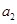 为整数知,等差数列
为整数知,等差数列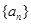 的公差
的公差 为整数.又
为整数.又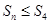 ,故
,故 于是
于是 ,解得
,解得 ,因此
,因此 ,故数列
,故数列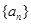 的通项公式为
的通项公式为 .
.
(2) ,
,
于是 .
.
考点:1.等差数列通项公式;2.裂项法求数列的前 项和.
项和.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
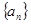 中,
中,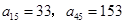 ,求数列
,求数列
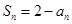 ,数列{bn}满足b1=1,b3+b7=18,且
,数列{bn}满足b1=1,b3+b7=18,且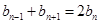 (n≥2).(1)求数列{an}和{bn}的通项公式;(2)若
(n≥2).(1)求数列{an}和{bn}的通项公式;(2)若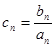 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.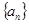 是首项为1,公差为2的等差数列,
是首项为1,公差为2的等差数列, 表示
表示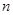 项和.
项和. 及
及 是首项为2的等比数列,公比
是首项为2的等比数列,公比 满足
满足 ,求
,求 .
. +n-4.
+n-4. 满足:
满足: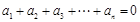 且
且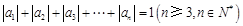 ,则称数列
,则称数列 阶“归化数列”.
阶“归化数列”.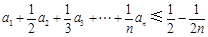 .
.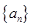 的前
的前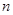 项和为
项和为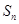 ,满足
,满足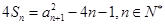 ,且
,且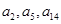 恰为等比数列
恰为等比数列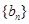 的前三项.
的前三项. 的前
的前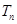 .
.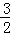 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.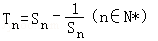 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.