题目内容
已知{an}前n项和为Sn,且Sn=1-an(n∈N*).(1)求数列{an}的通项公式;
(2)若
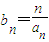 (n∈N*(5))求数列{bn}的前n项和为Tn.
(n∈N*(5))求数列{bn}的前n项和为Tn.
【答案】分析:(1)利用递推公式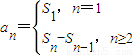 可得an与an-1的关系,结合等比数列的通项可求
可得an与an-1的关系,结合等比数列的通项可求
(2)结合数列的特点,考虑利用错位相减可求数列的和
解答:解(1)当n=1时,a1=1-a1,
∴a1= ,(2分)
,(2分)
∵Sn=1-an,①
∴Sn+1=1-an+1,②
②-①得 an+1=-an+1+an,
∴an+1= an(n∈N*),(4分)
an(n∈N*),(4分)
∴数列{an}是首项为a1= ,公比q=
,公比q= 的等比数列,
的等比数列,
∴an= •(
•( )n-1=(
)n-1=( )n(n∈N*).(6分)
)n(n∈N*).(6分)
(2)bn=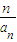 =n•2n(n∈N*),(7分)
=n•2n(n∈N*),(7分)
∴Tn=1×2+2×22+3×23+…+n×2n,③
2Tn=1×22+2×23+3×24+…+n×2n+1,④(9分)
③-④得-Tn=2+22+23+…+2n-n×2n+1
=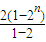 -n×2n+1,
-n×2n+1,
整理得 Tn=(n-1)2n+1+2,n∈N*.(12分)
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,解题的关键是利用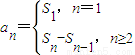 实现数列的和与项之间的相互转化,而一个数列的通项为anbn,且an,bn一个为等差数列,一个为等比数列时,求和用错位相减
实现数列的和与项之间的相互转化,而一个数列的通项为anbn,且an,bn一个为等差数列,一个为等比数列时,求和用错位相减
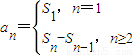 可得an与an-1的关系,结合等比数列的通项可求
可得an与an-1的关系,结合等比数列的通项可求(2)结合数列的特点,考虑利用错位相减可求数列的和
解答:解(1)当n=1时,a1=1-a1,
∴a1=
 ,(2分)
,(2分)∵Sn=1-an,①
∴Sn+1=1-an+1,②
②-①得 an+1=-an+1+an,
∴an+1=
 an(n∈N*),(4分)
an(n∈N*),(4分)∴数列{an}是首项为a1=
 ,公比q=
,公比q= 的等比数列,
的等比数列,∴an=
 •(
•( )n-1=(
)n-1=( )n(n∈N*).(6分)
)n(n∈N*).(6分)(2)bn=
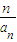 =n•2n(n∈N*),(7分)
=n•2n(n∈N*),(7分)∴Tn=1×2+2×22+3×23+…+n×2n,③
2Tn=1×22+2×23+3×24+…+n×2n+1,④(9分)
③-④得-Tn=2+22+23+…+2n-n×2n+1
=
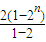 -n×2n+1,
-n×2n+1,整理得 Tn=(n-1)2n+1+2,n∈N*.(12分)
点评:本题主要考查了利用数列的递推公式求解数列的通项公式,解题的关键是利用
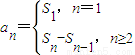 实现数列的和与项之间的相互转化,而一个数列的通项为anbn,且an,bn一个为等差数列,一个为等比数列时,求和用错位相减
实现数列的和与项之间的相互转化,而一个数列的通项为anbn,且an,bn一个为等差数列,一个为等比数列时,求和用错位相减 
练习册系列答案
相关题目